机器人运动学包括正向运动学和逆向运动学,正向运动学即给定机器人各关节变量,计算机器人末端的位置姿态; 逆向运动学即已知机器人末端的位置姿态,计算机器人对应位置的全部关节变量。一般正向运动学的解是唯一和容易获得的,而逆向运动学往往有多个解而且分析更为复杂。机器人逆运动分析是运动规划不控制中的重要问题,但由于机器人逆运动问题的复杂性和多样性,无 法建立通用的解析算法。逆运动学问题实际上是一个非线性超越方程组的求解问题,其中包括解的存在性、唯一性及求解的方法等一系复杂问题。
位姿描述表示机器人的位姿主要是指机器人手部在空间的位置和姿态,有时也会用到其他各个活动杆件在空间的位置和姿态。位置可以用一个位置矩阵来描述。
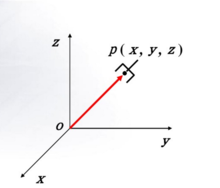

姿态可以用坐标系三个坐标轴两两夹角的余弦值组成的姿态矩阵来表示。
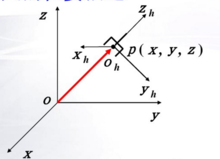

举个例子:
右图所示的两坐标系的姿态为


机器人的坐标系包括手部坐标系,机座坐标系,杆件坐标系,绝对坐标系。
手部坐标系:参考机器人手部的坐标系,也称机器人位姿坐标系,它表示机器人手部在指定坐标系中的位置和姿态。
机座坐标系:参考机器人基座的坐标系,它是机器人各活动杆件和手部的公共参考坐标系。
杆件坐标系:参考机器人杆件的坐标系,它是在机器人每个活动杆上固定的坐标系,随杆件的运动而运动。
绝对坐标系:参考工作现场地面的坐标系,它是机器人所有构件的公共参考坐标系1。
手部坐标系{h};机座坐标式{0};杆件坐标系{i}(i-1,2,...n);绝对坐标系{B}。
运动学方程概念机器人运动学的一般模型为:
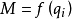 其中,M为机器人末端执行器的位姿,
其中,M为机器人末端执行器的位姿,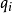 为机器人各个关节变量。
为机器人各个关节变量。
若给定 ,要求确定相应的M,称为正运动学问题,简记为DKP。相反,若已知末端执行器的位姿M,求解对应的关节变量,称为逆运动学问题。简记为IKP。
,要求确定相应的M,称为正运动学问题,简记为DKP。相反,若已知末端执行器的位姿M,求解对应的关节变量,称为逆运动学问题。简记为IKP。
求解正运动问题,是为了检验,校准机器人,计算工作空间等;求解逆运动问题,是为了路径规划,机器人控制,但求解比较困难。
举例建立三自由度平面关节机器人如图所示,设机器人杆件1,2,3长度为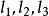 ,建立机器人的运动学方程。
,建立机器人的运动学方程。

1、建立坐标系
机座坐标系{0};杆件坐标系{i};手部坐标系{h}与末端坐标系{n}重合。

2、确定参数
各个轴线相互平行,各个杆件处于同一平面内。
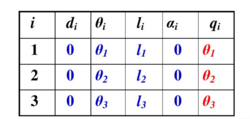
3、相邻杆件位姿矩阵
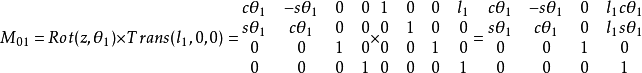
同理可得:
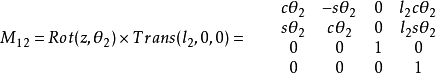
同理可得:

4、建立方程
将相邻杆件位姿方程依次相乘,则有
 式中,
式中,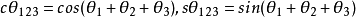
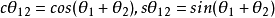
为了说明位姿矩阵中各个元素的作用,可以写为:
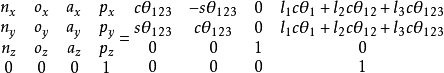 若用方程组表示,则为:
若用方程组表示,则为:
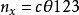


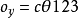

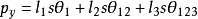




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国