[科普中国]-方向可调滤波器

方向可调滤波器具有任意旋转的功能，并可简单地表示为一组基滤波器的线性组合。由这种滤波器及其 Hilbert 变换形成的正交滤波器组，可以准确地检测出目标的边缘、纹理以及奇异点等特征。

方向可调滤波器对应的滤波器基是在频域上相互之间有一定重叠的一组滤波器，其中的每一个基滤波器都可表示为方向可调滤波器旋转到某一角度时的形式。在这里，选取二维高斯函数的一阶导数作为“基滤波器”，如下式所示：

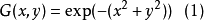
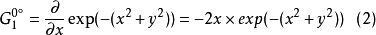
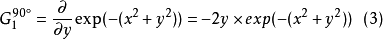式（1）为高斯函数，式（2）为 0°方向的基滤波器，式（3）为 90°方向的基滤波器，对（2）和（3）进行线性组合，即可得到任意方向的滤波输出，如下式所示：

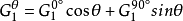
其中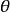， 是方向可调滤波器的方向输入。1

假定源图像中混有一定的加性孤立噪声，这种噪声往往是一些单像素奇异点。对这些奇异点，可以采用全局中值滤波的方法来剔除，但这种方法存在一个弱点，即在消除噪声点的同时，也削弱了图像中的特征。如果对图像进行一次预处理，找出图像中可能的噪声点，从而只在这些噪声点处进行局部中值滤波，那么源图像的特征可以较好地保存下来，而绝大部分噪声被滤去。

根据方向可调滤波器的原理，在图像中同时满足以下2个条件的，可以判定为孤立噪声点。

（1）由于噪声点与特征一样，也具有较大的奇异性，因此其局部方向能量很大。

（2）对于孤立噪声点，由于不具备很强的方向性，因而各个方向上的方向能量相差不大。即在孤立噪声点，方向能量的最小值与最大值之间比较接近。如果使用上节中设计的方向可调滤波器来分析每幅源图中的方向能量，则在各个噪声点处，与最小方向能量对应的方向垂直于主要方向。2

边缘检测是最早应用的图像分割方法。它通过检测图像上不同区域交界处的亮度变化实现图像中不同对象的分割。按数据的处理顺序可以将边缘检测方法分为串行方法和并行方法。前者从特定的初始点的邻域中按一定方向和规则寻找边缘点，再将找到的边缘点作为新的初始点继续寻找，重复这一过程可以得到连续的边缘线条。后者则仅凭借目标点及其周围若干像素的亮度来判断边缘点。

梯度计算法是最简单的边缘检测方法，它利用方向导数滤波器计算图像梯度借以判断边缘位置，是一种并行方法。经典的梯度算子如Sobel算子，根据其直观意义给出在相隔90°的两个基本方向上算子，如下图：

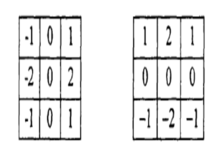
在这种情况下,为了得到其他方向上的方向导数，需要使用矢量合成的方法。其原理如下：

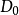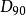分别利用0°和90°方向上的算子计算两个方向上的方向导数，分别记作和，则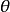方向上的方向导数计算值为：

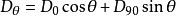梯度大小的计算值为：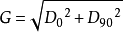

求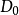和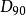都需要对于整幅图像进行模板运算，所以用这种方式求取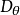就需要两次模板运算。模板运算的运算量相当大，由此产生了直接计算任意方向上的方向导数的需求。满足这一需求的方法是直接构造任意方向上的方向导数滤波器，如Kirsch滤波器，具有8个基本方向。3

clc;

close all;

clear all;

theta = [0:15:360];

inImg = imread('example.png');

dim = ndims(inImg);

if(dim == 3)

%Input is a color image

inImg = rgb2gray(inImg);

end

I = inImg;

tic

for i = [1:length(theta)]

J1(:,:,i) = steerGaussFilterOrder1(I,theta(i),3,true);

end

toc

tic

for i = [1:length(theta)]

J2(:,:,i) = steerGaussFilterOrder2(I,theta(i),3,true);

end

toc4