[科普中国]-鲁棒预测控制

鲁棒预测控制技术简介及发展背景

从MPC 过渡到NMPC（非线性预测控制），从技术发展的纵向来看，一些新的预测控制技术近年来也得到了蓬勃发展。这类预测控制技术主要体现在传统MPC和鲁棒、自适应等技术的结合。这类技术继承了MPC 的控制思想，通过算法参数的（自）调整、参考模型的在线修正和启发性建模等手段，从而回避了NMPC 发展中所遇到的非线性理论中存在的重重困难，有效地将模型预测控制技术扩展到了非线性控制领域。就如何处理带有不确定性的过程对象的问题上，通常有两类处理方法：一是采用“未雨绸缪”的策略，即使用鲁棒控制算法，在算法设计初期就将系统的不确定性考虑进去，使得整个控制系统在实际控制中面对对象不确定时仍能表现出应有的稳定性；另一类则采用“随机应变”的策略，即系统辨识技术，主动修正控制器本身的参数和策略，使得在新的控制环境中仍能得到令人满意的控制效果。1

软件产品及其应用对于工程应用而言，非常有必要研究并开发计算代价比较低廉的MPC 鲁棒综合技术，并使之适用于在线实施。尽管鲁棒控制的研究如火如荼，但应用却寥寥无几，特别是鲁棒预测控制的应用更是凤毛麟角。HoneyweII 公司推出的RMPCT中明确提到了鲁棒模型预测控制，并在文献中首次给出了RMPCT 在杜邦公司尼龙固相聚合反应釜中的应用实例，但其中对于系统鲁棒性的讨论却很少。1

发展历程模型不确定性对于可精确描述的过程对象而言，开环的最优化控制可以得到近乎完美的控制性能。事实上，开环控制系统面临着两大问题：①开环控制的本质决定了它无法对控制通道中存在的负载扰动、噪声进行抑制；②由于真实的过程对象很难使用精确的数学模型进行表述，最优控制的控制效果将大打折扣。第一个问题直接促进了反馈控制技术的发展，目前已经发展为相当成熟的理论。后者，即针对模型偏差和不确定性的控制的研究，导致了鲁棒控制技术的诞生，并已成为过程控制界的一个热门研究。

鲁棒控制的模型不确定性的假设有着鲜明的工程意义：从模型结构简化和控制实时性的考虑，在大多数的控制问题中使用固定模型结构的线性简化模型（称为“标称模型”），由此导致模型和（非线性）真实对象之间在动态性能上存在的显著差异。

由于真实对象的不可知性，使用线性化参考模型的传统的预测控制在进行模型响应的动态预测时，很自然地引入了更多的控制质量下降。尽管预测控制中引入了反馈校正机制，试图最大程度地减小模型中的不确定因素，然而，对于具有强非线性和不确定性的控制过程而言，这种使用线性化预测校正的机制无法从本质上将传统意义上的预测控制技术很好地应用于模型不确定控制场合。1

产生背景鲁棒预测控制技术是当使用线性参考模型的预测控制理论在非线性控制过程中的应用受到质疑的情况下诞生的，并且目前有关鲁棒预测控制的文献已经浩如烟海。有关无约束的MPC 的鲁棒稳定性早在1982 年Garcia 和Morari 的文献中进行了分析并且导出了保证系统的鲁棒稳定性的内模控制滤波器的调整策略。PoIak和Yang 在文献中具体讨论了MHC（MovingHorizon ControI）的鲁棒稳定问题，对象为采样时间可变的连续时间线性系统。文献中鲜明地表述了对象的不确定性，并把在线约束的最小化问题转换成一个最小最大问题来解决。1

综合问题研究由对MPC 鲁棒性能研究的回顾中可以看出，MPC 的鲁棒性能分析问题得到了很多的重视，也取得了一些有意义的成果，然而关于鲁棒综合问题仅有少数的文献加以讨论，而且都局限于FIR 模型。直到将线性矩阵不等式（LMI）技术引入到鲁棒预测控制研究框架之后，鲁棒MPC 的研究又注入了新的活力。将鲁棒优化问题及各种约束转换成线性矩阵不等式，利用成熟的求解算法即可对鲁棒优化问题进行快速求解计算。1

鲁棒无约束预测控制研究思路􀁚以不变集、LMI等作为基本工具。

􀂾将线性矩阵不等式（LMI）理论引入min-max预测控制的研究中，它比FIR模型更适用描述更为广泛的不确定性。

研究凸多面体**(**多胞）不确定模型、结构化反馈不确定模型，采用基于LMI理论的MPC综合方法，将min-max问题转化为包含LMI的min问题，同时考虑输入输出约束。

鲁棒预测控制算法考虑如下线性时变系统

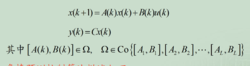
鲁棒预测控制算法描述如下：

在采样时刻k，将MPC的min优化问题变为min-max优化问题，求解控制律在不确定集中最坏情况下的目标函数值极小，即

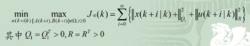
但J∞（k）难于求解，在一定条件下可以将上述极大极小问题转化为极小化鲁棒性能指标上界。

鲁棒性(Robustness)无论是对于何种形式的预测控制算法, 鲁棒性研究一直是其理论研究中的薄弱环节。实际工业过程存在于不确定性环境, 总会受到预先未知的各种不确定性的影响;模型和被控对象之间也不可避免地存在着失配。基于模型设计的最优控制律应用于实际对象可能导致系统性能变差, 因此研究MPC 鲁棒性是十分必要且有实际意义的。总的来说,MPC 鲁棒性问题的研究分鲁棒分析和鲁棒综合两个方面。2

MPC 鲁棒性分析Garcia 和Morari 于80 年代初提出在IMC 框架下研究MPC 性能, 并简单分析了MPC 系统的鲁棒性，推导了预测控制在内模控制结构下的定量表达, 然后由模型和对象之间的失配来分析鲁棒性, 其优点是可以定量地研究设计参数与系统鲁棒性间的关系, 但较局限。在上述基础上, 又研究了一类MPC 系统在模型增益失配和时滞失配时的鲁棒性, 给出了增益和时滞的允许失配范围, 以及失配度变化趋势和系统鲁棒稳定性的关系, 但所得定理只是充分的, 且仅针对这一类系统。随后, 以对象到闭环系统特征多项式的系数映射为基础, 分析了CARIMA 模型中噪声滤波器T 对于闭环系统鲁棒性的影响, 并通过比较得出GPC 中噪声滤波器T 作为设计参数时, 其地位实际上相当于DMC 中的校正参数, 它们都对模型失配时的闭环系统鲁棒性产生很大影响。2

MPC 鲁棒综合鲁棒综合问题是建立在被控对象模型不确定性描述基础上的。大多数鲁棒MPC 设计都基于min-max 描述, 具有H ∞控制的思想, 即将MPC 的在线min 优化问题变为min-max优化, 求解控制律使在不确定性最坏情况(worst case)下的目标函数值最小。根据目标函数和不确定性描述的不同, 可将鲁棒MPC 设计分为如下三类:

1)基于不确定FIR 模型的min-max 设计。

2)基于LMI 的MPC。

3)滚动时域H ∞控制。2