[科普中国]-简约KMP算法

简介

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特-莫里斯-普拉特算法（简称KMP算法）。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。因其操作方法简单，又称简约KMP算法。

kmp算法完成的任务是：给定两个字符串O和f，长度分别为n和m，判断f是否在O中出现，如果出现则返回出现的位置。常规方法是遍历a的每一个位置，然后从该位置开始和b进行匹配，但是这种方法的复杂度是O(nm)。kmp算法通过一个O(m)的预处理，使匹配的复杂度降为O(n+m)。

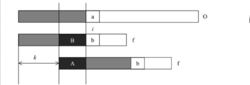
思想我们首先用一个图来描述kmp算法的思想。在字符串O中寻找f，当匹配到位置i 时两个字符串不相等，这时我们需要将字符串f向前移动。常规方法是每次向前移动一位，但是它没有考虑前i-1位已经比较过这个事实，所以效率不高。事实上，如果我们提前计算某些信息，就有可能一次前移多位。假设我们根据已经获得的信息知道可以前移k位，我们分析移位前后的f 有什么特点。我们可以得到如下的结论：

1、A段字符串是f的一个前缀；

2、B段字符串是f的一个后缀。

3、A段字符串和B段字符串相等。

所以前移k位之后，可以继续比较位置i的前提是f的前 i-1个位置满足：长度为i-k-1的前缀A和后缀B相同。只有这样，我们才可以前移k位后从新的位置继续比较。

所以kmp算法的核心即是计算字符串f每一个位置之前的字符串的前缀和后缀公共部分的最大长度（不包括字符串本身，否则最大长度始终是字符串本身）。获得f 每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和字符串O比较。当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将字符串f 向前移动(已匹配长度-最大公共长度)位，接着继续比较下一个位置。事实上，字符串f的前移只是概念上的前移，只要我们在比较的时候从最大公共长度之后比较f和O即可达到字符串f 前移的目的。

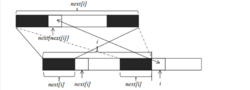
数组计算理解了kmp算法的基本原理，下一步就是要获得字符串f每一个位置的最大公共长度。这个最大公共长度在算法导论里面被记为next数组。在这里要注意一点，next数组表示的是长度，下标从1开始；但是在遍历原字符串时，下标还是从0开始。假设我们现在已经求得next[1]、next[2]、……next[i]，分别表示长度为1到i的字符串的前缀和后缀最大公共长度，现在要求next[i+1]。由上图我们可以看到，如果位置i和位置next[i]处的两个字符相同（下标从零开始），则next[i+1]等于next[i]加1。如果两个位置的字符不相同，我们可以将长度为next[i]的字符串继续分割，获得其最大公共长度next[next[i]]，然后再和位置i的字符比较。这是因为长度为next[i]前缀和后缀都可以分割成上部的构造，如果位置next[next[i]]和位置i的字符相同，则next[i+1]就等于next[next[i]]加1。如果不相等，就可以继续分割长度为next[next[i]]的字符串，直到字符串长度为0为止。

字符串匹配计算完成next数组之后，我们就可以利用next数组在字符串O中寻找字符串f的出现位置。匹配的代码和求next数组的代码非常相似，因为匹配的过程和求next数组的过程其实是一样的。假设现在字符串f的前i个位置都和从某个位置开始的字符串O匹配，现在比较第i+1个位置。如果第i+1个位置相同，接着比较第i+2个位置；如果第i+1个位置不同，则出现不匹配，我们依旧要将长度为i的字符串分割，获得其最大公共长度next[i]，然后从next[i]继续比较两个字符串。这个过程和求next数组一致。1

算法代码求next数组的代码如下：

void get_next(string pattern, int next[]) {

int i = 0;

int j = 0; // j == -1

next[0] = -1; // next[0]

int p_len = pattern.length();

while (++i

if (pattern[i] == pattern[j]) {

next[i] = j++;

} else {

next[i] = j;

j = 0;

if (pattern[i] == pattern[j]) {

j++;}}

int j = 0;

next[0] = -1;

int p_len = pattern.length();

int matched = 0;

while (++j = 0) {

if (pattern[curLeft] == pattern[curRight]) {

matched++;

curLeft--;

curRight--;} else {

matched = 0;

curLeft = --left;

curRight = right; } }

next[j] = matched;

matched = 0; }}}

根据next数组求模式串在主串中的位置代码如下：

int search(string source, string pattern, int next[])

{

int i = 0;

int j = 0;

int p_len = pattern.length();

int s_len = source.length();

while (j

{ if (j == -1 || source[i] == pattern[j])

{ i++;

j++; }

else { j = next[j]; } }

if (j

else

return i - pattern.length();}

举例举例来说，有一个字符串”BBC ABCDAB ABCDABCDABDE”，我想知道，里面是否包含另一个字符串”ABCDABD”

首先，字符串”BBC ABCDAB ABCDABCDABDE”的第一个字符与搜索词”ABCDABD”的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

因为B与A不匹配，搜索词再往后移。

就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

接着比较字符串和搜索词的下一个字符，还是相同。

直到字符串有一个字符，与搜索词对应的字符不相同为止。

这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把”搜索位置”移到已经比较过的位置，重比一遍。

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是”ABCDAB”。KMP算法的想法是，设法利用这个已知信息，不要把”搜索位置”移回已经比较过的位置，继续把它向后移，这样就提高了效率。

改进KMP算法是串匹配算法中效率较高的，它充分利用模式信息，使得模式在跟主串匹配过程中主串的指针不回溯，从而具有较高的匹配速度，并在各种领域中有广泛应用。然而，KMP算法仍存在着主串与模式多个相同字符重复比较的缺陷。在KMP算法的基础上，提出一种改进的模式匹配算法，可以减少比较次数，提高匹配效率。

算法基本思想：引入模式串的Q(r)函数，在模式中就双端分别求Q(r)函数值，根据模式两端当前字符的Q(r)函数值，使模式交替向中间滑动尽可能远的一段距离后，继续匹配1。