[科普中国]-复合混沌系统

1973年，Li和Yorke使用混沌(chaos)一词来研究混沌的特性，从而拉开了混沌研究的序幕。30年来，混沌已经成为一项热门话题。非线性动力学已经成为内容极为丰富，应用范围极其广泛的研究领域。混沌现象是发生在确定性系统中的一种不确定行为，具体表现在混沌系统具有分维吸引子和对初值敏感性，由于非线性动力学系统的运动状态失稳而出现分岔以至于混沌状态是非常普遍的现象。1

文献2提出了混沌可加性的概念，从理论上证明两个或两个以上混沌序列的可加性，计算机模拟表明新的混沌系统动力学行为具有分维吸引子和对初值敏感性。

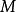若有 个混沌系统 ，其动力学差分方程为 ，

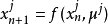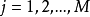
首先考虑两个混沌系统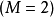 ，则上式可以改写为：

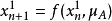
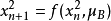复合构成的新系统的基本形式为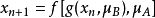

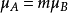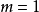设 ，如果 ，且两个混沌系统的系统参数相等，则完全相同结构的复合形式混沌系统为

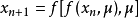
如果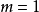 ，且两个混沌系统为不同结构，则复合结构的新混沌系统为：

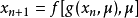
二维混沌系统的两个变量方向上分别有两种复合形式，在 变量方向上

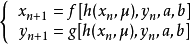在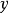 变量方向上，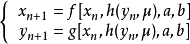

以上给出了两种一维混沌系统及其两种一维和二维混沌系统的复合构成方式。由于混沌系统的复合形式很多，尤其是高维混沌系统和不同结构混沌系统的多重复合更为复杂。

各种复合系统的分岔序列和简单混沌系统的分岔序列有相似的规律，可以使用不动点的确定方法和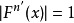 得出具体的分岔序列。1

以复合混沌系统在加密系统方面的应用为例。

近年来，利用混沌来研制新的加密系统引起了人们的广泛重视。由于混沌系统对初值条件和系统参数非常敏感，其生成的混沌序列具有宽频谱、类噪声、可精确再生和难以长期预测等特点，使混沌在加密和保密通信中具有潜在的应用价值。因此，借助混沌系统可望设计出容易控制和具有高安全性的加密系统。

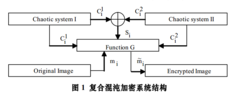
复合混沌加密系统如图1所示。图1中混沌系统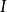 由Chen系统构成，混沌系统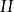由Logistic混沌映射构成，两个系统分别在第i时刻输出混沌序列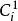和。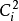

序列产生规则如下：

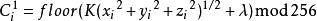
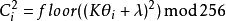
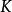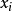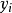其中，，和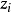是Chen系统的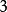个状态变量在第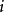时刻的值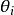，为Logistic系统在第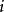时刻的值，而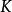和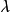为控制参数。混沌系统对初值条件很敏感，但是当初值条件有微小差异时，这种敏感性是需要系统经历一段演化时间才会充分体现出来。因此，为了适应图像这种大数据量对加密速度的需求，用一个因子去放大这种敏感性。3