在离散型随机变量中,计算变量的每个可能取值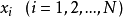 的概率,求得的结果即为分布律,满足下式:
的概率,求得的结果即为分布律,满足下式:
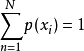
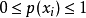
在连续型随机变量中,概率密度函数(在不至于混淆时可以简称为密度函数)是一个描述这个随机变量 的输出值在某个确定的取值点附近的可能性的函数。
的输出值在某个确定的取值点附近的可能性的函数。
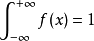
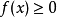
设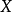 是一个随机变量,
是一个随机变量, 是任意实数,函数
是任意实数,函数
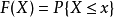 称为
称为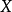 的分布函数(累积概率分布函数)
的分布函数(累积概率分布函数)
具有的性质如下:
1)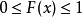
2)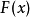 是
是 的不减函数1
的不减函数1
在区间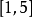 上任意掷一个质点,用
上任意掷一个质点,用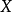 表示这个质点与原点的距离,则
表示这个质点与原点的距离,则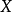 是一个随机变量。如果这个质点落在
是一个随机变量。如果这个质点落在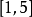 上任一子区间内的概率与这个区间的长度成正比,求
上任一子区间内的概率与这个区间的长度成正比,求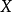 的分布函数。1
的分布函数。1
解:
由题意知,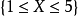 是一个必然事件,则
是一个必然事件,则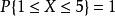
若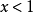 ,则
,则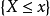 是不可能事件,
是不可能事件,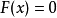
若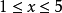 , 则
, 则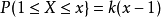 ,特别的,取
,特别的,取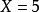 ,由
,由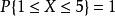 ,可得,
,可得,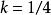
从而
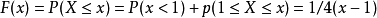 若
若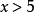 ,则
,则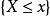 是必然事件,
是必然事件,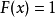
综上所述:

设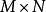 像素大小图像的最大灰度级为
像素大小图像的最大灰度级为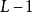 ,图像的灰度直方图
,图像的灰度直方图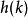 为具有灰度级
为具有灰度级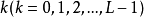 的像素个数。灰度级分布概率
的像素个数。灰度级分布概率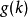 的值是
的值是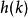 除以图像总的像素个数。图像的累积概率分布
除以图像总的像素个数。图像的累积概率分布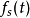 为
为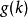 的前
的前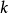 项
项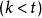 之和,表示为:
之和,表示为:
 其中,
其中,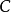 ——
——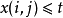 的个数,
的个数, ——图像在像素
——图像在像素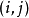 处的像素值,
处的像素值,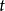 ——图像灰度级。2
——图像灰度级。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国