[科普中国]-天然气状态方程

理想气体状态方程

理想气体的假设：

1、气体分子本身所占的体积比起整个气体体积来说是可以忽略不计；

2、所有气体分子间的碰撞以及分子与器壁的碰撞是纯弹性的；

3、气体分子之间以及分子和容纳它的器壁之间不存在引力或排斥力。

对于以上条件下的，称之为理想气体，它将遵守如下定律：

波义尔定律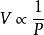： 或PV=C（当T为常数时）

盖·吕萨克定律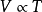： 或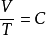 （当P为常数时）

查理定律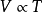： 或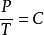 （当V为常数时）

根据以上定律可推导出理想气体状态方程为：

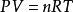
范德华方程式对于实际气体来说，除低压条件下近似服从理想气体状态方程式外，一般都与理想气体状态方程式发生偏差，有时甚至发生较大的偏差。

这是因为实际气体的分子间具有作用力。在低压时，分子与分子间距离较大，作用力可以忽略不计。当处于高压时，分子间的距离缩短了，其相互间作用力已经不能忽略。

对于理想气体曾假设分子本身的体积比起总体积来小到可以忽略不计，这在压力很低时，可以近似地认为是这样。然而实际上当气体密度随压力增高而增大时，分子所占的体积就不能忽略不计了。

范德华考虑了实际气体的上面两种情况，对理想气体状态方程式进行了修正：

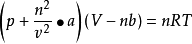式中

a、b是取决于气体类型的常数。1

实用气体状态方程在高压下必须对理想气体状态方程进行修正, 即引入一系数Z, 从而得到天然气的压缩状态方程为:

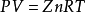
式中, Z 通常称为压缩因子, 它是给定压力和温度下, 实际气体占有的体积与相同压力和温度下的理想气体所占有的体积之比。

实际气体由于分子本身具有体积, 故较理想气体不易压缩; 而分子间的引力又使实际气体较理想气体易于压缩。压缩因子Z 的大小恰恰反映出这两个相反因素的综合结果。当Z 值大于1 时, 即气体较理想气体难压缩; 而当Z 值等于1时, 实际气体成为理想气体。Z 值大小与气体性质、温度和压力有关, 通常必须用实验测出, 做成图版备查, 也可以用相关式计算。

应用对应状态定律在气体参数计算中应用也相当广泛。其内容是: 在相同的对应温度和对应压力下, 所有的纯烃气体具有相同的压缩因子。这里的对应温度和对应压力是指气体的温度与压力分别除以该气体的临界温度和临界压力所得的比值。1