[科普中国]-非线性奇异系统

基本概念非线性系统

所谓非线性系统，指的是系统的状态与输出变量在外部条件的影响下，不能用线性关系来描述的系统。系统受到的这种影响是相对于系统输入的运动特性来说的。由于组成系统的各部件在不同程度上存在非线性的性质，因此在实际生活中，绝对线性的系统是不存在的。为了改善系统的这种非线性性以得到稳定的系统，需要通过设计控制器来研究系统的稳定性，由此产生了相平面法、描述函数法和谐波平衡法等。在过去的几十年里，对于非线性系统的研究，产生的很多新兴的控制理论中，普遍结合了李雅普诺夫稳定性理论，例如以Kokotovic为代表的反推控制理论(Backstepping ) ，以意大利Isidorii教授为代表发展起来的微分几何控制理论，以Swaroop和Hedrick等人为代表基于反推控制理论发展起来的动态面控制设计方法，以Zade和Mamdani教授为代表发展起来的模糊数学和模糊控制理论。迄今为止，李雅普诺夫方法己经成为研究非线性系统最常用也是最为完善的一种方法，通过构造李雅普诺夫泛函、构造系统控制器来研究非线性系统的稳定性也己取得显著成效。

奇异系统奇异系统(singular systems)是一类由微分及代数方程综合描述的系统，它在结构形式上比仅由纯微分方程或差分方程描述的正则系统多了代数方程描述部分。由于研究领域的不同，奇异系统又被不同领域的学者冠以不同的称呼，例如广义状态空间系统、描述系统等等。由于奇异系统描述比正常系统多了代数方程描述部分(快变子系统)，因此，奇异系统的适用度比正常系统要广泛得多。通过系统适当地变换，奇异系统也可以描述成正则系统，但是，许多原有系统的物理特性在变换后有可能会丢失。

最早的奇异系统模型是由学者Ardema在1962年通过研究航天器的动力模型过程中提出的。后来，Rosenbrock在研究复杂的电网系统时，发现电网中某些部件突然失效，在失效的前后时刻有电流的瞬动现象产生，这种瞬间变化的现象不包括在常见正则系统描述之中，在经过大量的研究及实验后，建立了电网系统的奇异模型。自此以后，广大研究爱好者对奇异系统展开了广泛地研究，并且获得了许多非常有价值的理论成果。由于奇异系统适合于描述规模较大且非常复杂的系统，因此，自上世纪八十年代开始奇异系统被非常广泛地用于奇异摄动系统、电子网络系统、决策系统、复杂大规模系统等各个领域。随着广大学者研究的不断发展和深入，许多可以由奇异系统描述的实际系统不断被发现。例如，受限机器人、纽曼模型、Leontief模型、非因果系统、核反应堆等均是典型的奇异系统。

目前，虽然大量的学者在奇异系统相关理论中取得了许多的理论研究成果，但是仍旧有不少的奇异系统理论分析与实际应用上的问题需要研究及解决。例如目前仍然没有获得时变奇异系统显式解等，同时，仍有许多研究成果令人不太满意，如时变时滞系统的稳定与镇定等。

数学描述奇异系统也被称为流形上的微分代数系统、广义系统、描述系统、广义状态空间系统或半状态空间系统等等。它的一般形式如下：

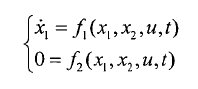
20世纪70年代，Rosenbrock在讨论复杂的电网系统时最先提出了奇异系统的问题。后来，Luenberger发现经济领域中有些问题也属于此范畴。在七十年代后期，奇异系统开始得到了广泛研究，迄今为止有三种典型方法用来研究奇异系统：状态空间法，几何方法和多项式矩阵法。状态空间法是基于奇异系统的状态方程，用于研究结构性质和设计控制器；几何方法由Wonham针对线性系统提出，由Lewis将其扩展到解决奇异系统的反馈控制问题；多项式矩阵法是基于传递矩阵的某种分解，应用到奇异系统的分析和观测器的设计上。

近年来，关于奇异系统的研究，己经取得了较大的进展，特别是在线性时不变系统，包括可解性、稳定性、能控性、能观性、极点配置、观测器设计、解祸、最优控制、分散控制在内的各种问题已经解决，建立了这相当完备的理论。对于线性时变奇异系统在过去十年也己取得了相当的成就。Cam户ell和Terrel的研究表明通过解析坐标变换可将线性时变奇异系统转化为标准正则形。

对于非线性奇异系统，还有更特殊的一类称为仿射的非线性奇异系统，其形式为：

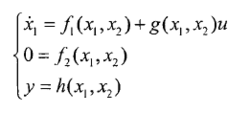
其中x1为状态向量，x2为代数向量，u为控制输入，y为量测输出变量。f1,f2,g,h是适当维数的光滑向量场，且h(0,0)=0， f1(0, 0)=0，f2(0, 0)=0。

此系统的特点是关于控制输入u为线性的。通过坐标变换和变量分组等，许多系统都能化成上式的形式。

实际应用人们发现非线性奇异系统有着广泛的实际应用背景，包括了完全和不完全受限机械系统、电路系统、化工系统等等。

特别是在机器人控制中，更涉及到非线性奇异系统。出现在力与位置控制任务中的运动约束的机器人系统，一个具有末端执行器的机器人，末端执行器必须保持和一个刚性面接触，在该面上末端执行器的接触力和位置须同时控制；两个操作同一物体的机器人，该物体的运动以及施加于该物体上的挤压力需同时控制;封闭链机械臂：行走机器人；利用多手指机器人进行的抓合协调运动等等。一般来说，机器人本身是一个强祸合的多变量控制系统，通常由非线性常微分方程来描述。但是，当机器人执行任务的过程中，常常因终端执行器同对象及环境接触而产生接触力。因此对机器人施加某些限制，这些限制通常由非线性代数方程来描述，使机器人的控制模型是一个非线性的微分代数方程，即非线性奇异系统。在机器人控制问题中，受限机器人、移动机器人及机器人的协调控制等都需用非线性奇异系统来描述。1