[科普中国]-网格自动生成

在连续的物理系统中，如在飞机周围的气流，水坝上水对水坝的集中压力，集成电路中电子的电场，或是在化学反应中的反应物的浓度等，都是需要应用偏微分方程来模拟的。想要在计算机上模拟这些系统，这些连续的方程需要首先离散化，结果产生一组由有限个离散点组成的空间或平面包括对应的时间序列，在这些点上，我们才可以分别对所要研究的变量，如电压，密度，和电场等进行计算。离散化的通常方法有有限差分，有限体积和有限元方法，这些方法通过相邻的点来计算出变量的导数。这些计算需要基于一定的网格来实现，所以网格的概念也就随之产生。

随着网格应用的不断广泛和深入，人们就自然而然产生了一种动机，要去实现和改进自动化网格生成算法。在起初的时候，应用有限元方法的人们用几十或是几百个网格单元来模拟一个很大的简化了的规则区域，他们己经感到很满意了。要把一块区域人工的划分成一系列有用的网格单元，这样的预处理工作非常的艰辛。而现在人们只需要点一下按钮，就可以通过软件来轻松的自动生成复杂的网格，这些网格包含了成千上万的网格单元，而不需要任何繁琐的预处理工作。1

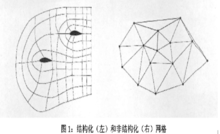目前为止，根据网格的连接关系来区分，主要有两大类结构化网格和非结构化网格。

结构化网格主要是指对每一个网格节点，其对邻接的其他节点的连接数是一定的或有规则的对一些网格，可能会有一线部分节点与其他节点的连接数是不同的。

非结构化网格是指的每一个网格节电与其他节点的连接关系是不确定的或不规则的。

图1给出了一个着两种不同形式的网格的一个简单例子。在有些情况下，整个网格的一部分可以是结构化的，而另一部分又是非结构化的譬如在河道流域中，边界上的网格是结构化的而流域内部是非结构化的。1

所谓结构化网格是指，它的网格所有节点的连接关系是规则的。例如，网格中的所有网格点能够通过索引方便的查找和确定(在二维中通过两个索引确定，三维中则是三个索引)。每个网格点的邻接点能够方便的同过索引计算出来，而不是去一一查找（例如，网格点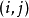 的邻接点就是 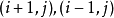等等）。在规则的矩形区域上的网格生成虽然简单，但其价值不大，规则的网格生成技术主要专注于对不规则的边界区域进行网格化，例如，血管中血的流向，或者血管得变形，金属中热量的传导等等。通常网格的生成必须符合它的边界，用某一面坐标来形成（部分）网格边界。这种方法在边界处可以提供精确的结果，速度也很快。对于流体研究中，这种网格可以作为波动模型的很好应用，因为流体研究中往往需要网格要和区域的边界很好的吻合起来。另外一种选择便是应用一个简单的矩形网格作为基础，在区域的边界处通过网格裁剪，使其符合边界的要求，然后对那些边界上不够理想的网格再用局部的修饰，从而得到我们的最终结果（笛卡尔网格）。这种方法在区域的边界处打断了网格的顺序，还要删除一些网格单元，这些都增加了网格生成算法的复杂度。迪卡尔网格的生成速度是很快的，在空气动力学中应用较多。但似乎不适用于 Navier-Stokes空气动力学。

生成区域边界固定网格的最常用方法是需要产生一个连续的，并在边界上完全符合的网格。也就是要找到一种方法，把一组连续毗邻的矩形可计算区域通过曲线边界映射到一个实际的物理区域如图2。

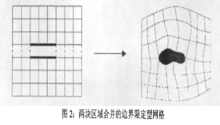
如果希望不添加任何额外不规则的偏斜网格，又能用一个映射关系把一个规则的矩形可计算网格映射到一个复杂的区域上，这几乎是非常困难的。为了要绕开这个问题，要把区域分成罗干个子区域，对每个区域再进行网格划分。在子区域与子区域的结合处，网格的连接必须要连续的。这就是多分块网格的主要思想。对于区域的分解，一般都通过工具手工完成，虽然这比较慢。

另外一种用多化分块思想来生成连续的边界拟合网格的方法是，在边界区域上，我们用固定边界的网格生成法，在区域的内部用规则的矩形网格，在两种网格较叉的区域，我们通过插值方法来使网格点相匹配。这样生成的网格叫Chimera网格。

Chimera网格对于移动的边界（例如，在直升机机翼叶片中）或多条边界混合（流动中的粒子）非常有用。因为这样网格的绝大部分网格单元始终都是固定的，而只有边界上通过插值的网格单元是随着边界的变化而变化的。Chimera网格却是有其独特的优点，最近守恒插值方法的发展又增加了它的有甩性。但是，一大批的结构化网格生成方法都是基于区域分块化思想，故下面主要是讨论这一思想方法的应用。1

1973年Gardon 和 Hall 2在多变量概念的基础上提出了生成网格的无限插值理论，缺点是不易控制物面附近的网格趋势。 1981年Eriksson 与 Rizzi 3提出改进的无限插值理论思想，即在文献2的基础上引进物面笛卡儿坐标变量关于物面逸出变量的导数，利用这些导数来控制物面附近的网格变换。

用这种理论构造网格时，需要：

1）定义边界上的网格分布

2）在物面上 构造上述导数

3）构造插值时需用的型函数

其中，2）是困难且关键的步骤。4

PDE方法可分为椭圆型 、抛物型及双曲型 3 种。

70 年代初，自 Thompson等人首先提出了求解偏微分方程生成贴体网格方法，并首次应用于二维物体绕流的数值计算以来，该方法已成为生成复杂几何外形贴体网格的主要技术。通过数值求解椭圆型方程生成曲线坐标系，由于椭圆型方程固有的可以光顺边界数据的特性，即抑制所求边界当地的不连续性向场内部的传递，从而使其成为一种非常有效的数值网格生成方法。采用求解椭圆型方程组技术，进 一步调整内部及边界网格的疏密分布和正交性，以满足黏流数值模拟和插值精度的需要。5

非结构化网格主要是为了有限元方法的应用而发展起来的。对于有限元方法，可以有很多适用于计算的单元体四面体单元、棱柱体单元、块状体单元，它们之间的连接关系是不定的，这种特性也就是非结构化网格的本质。但是，其中能够完全的通过自动化过程来生成网格的单元只有三角形二维空间、和四面体三维空间。虽然方块单元是理想的，但对于方块单元要想完全自动化生成网格是很困难的必须在区域的某些地方加入棱柱体或四面体来补充。1

映射法出现于 20 世纪 70 年代，是最早采用的网格生成方法。从 70 年代开始应用于商品化系统中，比如 FEM GEN。目前映射法在现有的商品化系统中仍占统治地位，它是根据形体边界的参数方程，利用适当的映射函数，将待分区域映射到参数空间中形成规则参数域，对规则参数域进行网格剖分，将参数域的网格 (二维是正方形 ，三维是立方体) 反向映射回欧氏空间，从而生成实际的网格。

映射法可分为三大类 :保角映射法、基于偏微分方程法、代数插值法。

三维网格划分的许多方法都是先将形体的表面离散化，所以曲面映射是三维映射的基础。在空间参数曲面网格的生成中，根据曲面边界的性质有单线性映射、双线性映射 、三线性映射。

映射法的优点是：计算效率高，网格分布均匀、排列整齐，便于直接生成四边形、六面体等高精度单元。但是，映射法对于形状较为复杂的形体适应性差，需要将复杂形体事先分解成若干形状简单的子域。子域分解繁琐费时，人工交互多，难以实现全自动化。6

结点连元法形成网格的过程是先布点，后将结点连线生成单元。随机布点法不能保证布点均匀，且点距检查计算耗时效率低；直接布点法中，长方形网格直接布点法和等距水平线扫描法虽然方法简单、算法快速、布点比较均匀，但单一死板，不能避免产生最后剩余的空白地带；硬币填充法布点均匀，能较好地避免产生最后剩余的空白地带。总的来讲，结点连元法的优点是：对于复杂形体适应能力强，与其他方法相比能容易实现网格生成的自动化，所以也有人将该方法直接叫做自动化网格划分方法，此外，该方法生成的单元形状良好；缺点是计算量大、效率低。6

这种方法实质上也是结点连元法。Delaunay三角划分在散乱数据场的可视化 、逆向工程 、地理信息系统 (如地貌的不规则网格建模) 、VRML 产品建模等领域都有十分广泛的应用，尤其在有限元网格自动生成方面广为流行。

在平面域的 Delaunay 三角划分中，理论上已经严格证明，只要给定的结点分布中不存在四点及四点以上共圆时，有最优解，即所有三角形单元中最小内角之和可达到最大值。在 Delaunay 三角划分后，形成许许多多彼此相连的 Voronoi 多边形，每个只有一个结点，每一个 Voronoi 多边形的边实际上就是其内结点与相临 Voronoi 多 边形内结点连线的中垂线，所有Voronoi 多边形的集合叫做 Dirichlet 图，连接相临Voronoi 多边形内的结点便形成三角形网格。

实现Delaunay 三角剖分的方法很多，常用的一种算法是逐个插入结点的递归算法。该算法要求生成Delaunay 三角形的外接圆内不允许存在其他结点，若有其他结点，则应局部修改原来的剖分。基本过程为：先构造一个大外接圆，将所有结点都包含进去，然后找出已有三角形中哪些三角形的外接圆内包含新加入的结点，删除这些三角形内离新结点距离最近的一条边，将新结点与周围的老结点连线形成新的三角剖分。6