[科普中国]-脊波导

脊波导分双脊波导和单脊波导, 如图所示。它可看作由矩形波导把宽壁弯折而成, 其中的电磁场模式与矩形波导的模式相似, 于是采用相同的模式名称, 只是在脊棱附近由于边缘效应使场分布受到扰动。

脊波导的主要参数有主模截止波长、脊波导单模工作带宽、脊波导特性阻抗 脊波导功率容量、脊波导衰减。1

在现代微波工程中，为了满足微波传输系统性能的某些需求，需要不断探索和研究具有特殊截面形状的各种新型波导。最近几十年来，由于脊波导具有低主模截止频率、宽频带和低阻抗特性，各种结构形状的脊波导应运而生。2

脊波导与相同尺寸的矩形波导比较主要优点是：主模H10波的截止波长较长, 对于相同的工作波长, 波导尺寸可以缩小 H10模和其它高次模截止波长相隔较远, 因此单模工作频带较宽, 可以达到数个倍频程；等效阻抗较低, 因此易与低阻抗的同轴线及微带线匹配；但脊波导承受功率比同尺寸的矩形波导低。1

横向谐振条件方程

当波导截止时, 电磁波将在两窄边之间来回反射, 形成谐振, 其横向传输线上任何参考面的总的电纳应该为零 在图中以T面为参考面, 得到图2的等效网络（a）、 （b） , 并由此写出谐振方程为奇模谐振方程和偶模谐振方程。

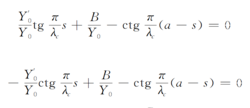
矩形波导跳变引起的电纳为

对于双脊波导当s 为有限值时，式( 4) 只需用截止波长λc代替式中的λg即可;对于单脊波导用λc/ 2 代替式中的λg；至此，当已知脊波导的截面尺寸后，则式( 1) ~、( 2) 就是以λc为未知量的超越方程，可以数值解计算脊波导截止波长λg 通过编制计算程序，解方程获得截止波长。

通常情况下，工程上选取的脊波导都要靠近一些标准，当双脊波导选b/a= 0.45，单脊波导选b/a= 0. 5时 我们可以查读工程应用曲线。并计算得双脊波导TE10模的截止波长λCTE10 单脊波导TE10模的截止波长λCTE10。1

脊波导的主模工作带宽定义为主模截止波长与邻近高次模截止波长之比 对于任意脊波导，其TE20模截止波长总是大于TE30模。脊波导的理论工作带宽为We= λCTE10 /λCTE20。应用查表的方法可以查到当双脊波导b/a= 0.45单脊波导b/a= 0. 5时的理论工作带宽We和TE10模的截止波长λCTE10再计算TE20模截止波长λCTE20。应用解方程的方法可以算出TE10波的截止波长λCTE10、TE20模截止波长λCTE20再求We。实际上电磁波的截止状态是一个渐变的过程。

经验得出: 脊波导的有用工作带宽Wf小于理论工作带宽。换算成频率范围为:

Δf= fmax - fmin = 0. 98fC20 - 1.18fC101

脊波导的特性阻抗是脊波导的重要参数之一 。它有不同的定义，有以电压与功率之比定义的特性阻抗，有以电压与电流之比定义的特性阻抗。在任意频率下的特性阻抗的一般表达式为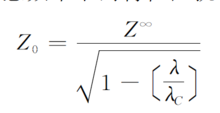

式中Z∞为频率无限大时脊波导特性阻抗;λ为自由空间波长; λC为脊波导的截止波长。1

理论最大功率容量:

式中 E0为脊波导横断面脊的中心线上的电场强度; m= 1 为双脊波导; m= 2 为单脊波导。选取的特性阻抗是电压与功率比定义的 特性阻抗值偏大，即功率容量值偏小。1

从40年代起，Cohn开始研究脊波导的特性。Hofper和Pyle在Cohn的基础上，分别用横向谐振法和准静态法对脊波导主模的截止波数作了计算，但对高次模却无能为力。随着人们认识到脊波导的宽带特性在通信等领域的重要作用，随后又有多种方法运用到脊波导的分析与求解。

有限元法是近似求解数理边值问题的一种数值技术，广泛应用于工程和数学问题。目前，二维问题的有限元方法已相当成熟，在电磁学和其他方面起着显著的作用。有限元法可以分析任意形状截面波导的特征值问题。