[科普中国]-数据采集处理系统

数据采集意义

数据采集是计算机信息处理的一个重要组成部分，是通过传感器、变化器等其他外部设备将压力、温度、光照强度、湿度等非电量信号转化为计算机能够识别的电量，将模拟信号转化为数字信号即A/D转换。这是一门有着极强实用价值的综合学科，在石油、汽车、航空航天、机械制造等方面有着广泛的应用。人们可以轻易地通过外部设备对需要的信号进行数据采集、数据处理、数据控制以及数据管理，进而对各种生产活动进行综合的一体化控制。在生产过程中，对工艺参数进行采集、检测，为提高产品质量、安全化生产、降低产品成本提供可行的信息支持。在各种科学研究中，通过数据的采集，可以获得不同的宏微观、动静态等数据信息，例如植物生产过程中所需要的温度、湿度、光照强度等数据信息的采集与处理。

组成数据采集系统一般是由传感器、放大电路、滤波器、多路模拟开关、采样/保持器、D/A转换器、计算机I/O接口以及定时与控制逻辑电路。传感器的作用是把外界的模拟量转化为计算机能接受的数字量；放大电路通过晶体管的放大作用，将放大和缓冲输入信号；滤波器用来衰减噪声，以提高输入信号的信噪比；多路模拟开关把多个模拟量参数分时接通，提高电脑工作效率；采样/保持器是保证了采样过程中信号的稳定，提高采样精度；D/A转换器是把输出的数字信号转变为模拟信号；计算机I/O接口是保证输入、输出信号顺利传输；定时与控制逻辑是控制各元器件的逻辑以及时间关系，保证各元器件能有序地工作。

特点计算机只能处理数字量，绝大多说的执行机构只能接收模拟量，因此需要在数据进入计算机之前将其转化为数字量（A/D转换），在其进入执行机构之前将其转化为模拟量（D/A转换）。采样过程中由于计算机的处理速度非常快，而模拟量的变化速度一般情况下都比较慢。因此，往往一台计算机采样同时控制多个参数，这些参数被计算机控制进行分时采样。在采集过程中，为了保证采集的不同参数量的独立性与完整性，需要用不同的开关去控制对应的参数量，而且计算机在某一时候只能接受某一特定的模拟量，再通过多路模拟开关进行切换，使不同的参数量通过不同的支路分时进入计算机，保证了计算机运行的高效性。在数据采集的过程中，如果模拟量的变化，将直接影响到计算机的采样精度。特别是在同步系统中，多个不相关的参数量取瞬态值的时候，而其A/D转换又是采用同一台计算机，那么采样得到的几个参数量就不是同一时刻的参数量，无法进行数据处理和比较。所以在采样的过程中就需要输入到A/D转换器的模拟量在整个数据采集过程中保持不变，而且要保证在转换之后，A/D转换器的输入信号能够随着参数量发生变化。

数据处理计算机中信息的计量单位在计算机中信息是以字节（Byte）来进行采集、存储、处理以及管理的，字节是计算机基本的计量单位。在在UTF-8编码中，一个英文字符等于一个字节，一个字节等于8位（bit），一个位反应二进制码中0和1的信息。存储容量通常用KB（千字节）、MB（兆字节）、GB（千兆字节）以及TB来表示。

1KB=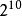 B=1024B

1MB=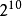 KB=1024KB=1048576B

1GB=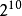 MB=1024MB=1048576KB

1TB=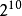 GB=1024GB=1048576MB

ASCII码是现当今电脑通用的单字节编码系统，任何的图片、文字以及图像/音频等信息都是反映在ASCII码中，在标准中一个字符占一个字节，一个汉子占两个字节。例如一张容量为1MB的软盘，能够储存的字符数为1024×1024=1048576（个），能够储存的汉字数为1024×1024/2=524288（个）。

数制以及转化数制是计数的规则，主要有二进制（B）、八进制（O）、十进制（D）以及十六进制（H），一般情况下，在用这些数制表示数字时通常要把英文字母代号写在后面。二进制是计算机应用最多的数制，因此需要研究数制之间的转化关系，才能较好地传递信息。

（1）十六进制转化为二进制。将十六进制的每一位当做二进制对应的的四位来处理，十六进制每一位有十六个数码，四位二进制数码总共十六位数，因此可以相互对应。例如8AH=（1×27+0×26+0×25+0×24）+（1×23+0×22+1×21+0×20）=10001010B。

（2）十进制转化为二进制。将十进制总体去跟2n去比较，当十进制数介于2n和2n+1之间时候，则用十进制除以2n得到余数依次去除2n-1、2n-2......直到余数为1或者0。例如20D=1×24+0×23+1×22+0×21+0×20=10100B。

（3）八进制转化为二进制。八进制每一位有八个数码，三维二进制数码共计八位数码，因此可以相互对应，可以将八进制的每一位当做二级制对应的三位来处理。例如740 =（1×25+1×24+1×23）+（1×22+0×21+0×20）=111100B。

（4）二进制转化为十进制。二进制数转化为十进制，需要将对应的位数乘以对应的2的阶数，然后累加就可以。例如：100111B=1×25+0×24+0×23+1×22+1×21+1×20 =32+0+0+4+2+1=39D。

（5）其他进制转化为十进制。其他进制转化为十进制，将对应位数上的数字乘以进制数的位阶数，然后累加就可以的得到。例如：103711O=1×85+0×84+3×83+7×82+1×81+1×80 =32768+0+1536+448+8+1=34761D。

（6）十进制转化为其他进制。十进制转化为其他进制，需要将将十进制总体去跟其他进制最高位的位阶数以及次高位的位阶数比较，当十进制在这两个数之间，则用十进制数一次去除以递减的次高位的位阶数，知道最后剩下的数字不大于其他进制的阶数上的最大数码。例如：13754D=12288+1024+384+56+2=3×84+2×83+6×82+7×81+2×80=32672O1。