[科普中国]-霍普菲尔德神经网络

核心思想

霍普菲尔德提出的神经网络模型有两个重要成分，即储存信息和提取信息。在典型的对称性霍普菲尔德模型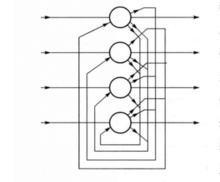中，其系统的动力学趋于使能量函数达到最小值，生物学的噪声或神经元的背景活动可用温度表征，这就使神经网络具有统计力学或热力学的特性。霍普菲尔德模型及其统计力学理论不仅增加了神经网络的理论概念，还发展了神经网络的计算方法，解决了网络中神经单元数与储存模式数量之间的关系，以及网络噪声与神经单元储存效率之间的关系。霍普菲尔德提出的能量函数和网络自由能概念是其理论的基石。网络从高能状态到达最小能量函数状态，则得到收敛，给出稳定的解，完成网络功能，这是该理论的核心思想。这种理论实际上把脑看成由大量结构简单、动作相同的单元组成，与固体物理学的模型——自旋玻璃(spin glass)相似，每个单元的方向和位置是随机的，由这些单元在相空间相互竞争所确定。对于整个网络来说，如果各神经元之间的联结强度是对称的，且其变化是非同步的，那么网络不断变化，进行迭代直至收敛于某一点；如果网络中全部神经元的变化是同步的，那么网络变化是周期性的；如果各神经元之间的联结是非对称性的，那么网络可出现定点收敛、周期性变化和混沌等三种状态。2

分类Hopfield神经网络按照处理输入样本的不同，可以分成两种不同的类型：离散型(DHNN)和连续型(CHNN)。前者适合于处理输入为二值逻辑的样本，主要用于联想记忆；后者适合于处理输入为模拟量的样本，主要用于分布存储。前者使用一组非线性差分方程来描述神经网络状态的演变过程；后者使用一组非线性微分方程来描述神经网络状态的演变过程。3

离散型的Hopfield网络是一种全反馈式网络，其特点是任一神经元的输出均通过联结权重反馈到所有神经元作为输入，其目的是让任一神经元的输出都能受所有神经元输出的控制，从而使各神经元的输出能够相互制约。2

连续型Hopfield网络的拓扑结构与离散型Hopfield网络相似，所不同的是，连续型Hopfield网络中节点的状态为模拟值且连续变化。基于生物存储器基本思想，Hopfield在1984年提出了连续时间的神经网络模型。4

特点霍普菲尔德(Hopfield)提出神经网络作为存储处理理论。霍普菲尔德网络具有以下特征：

1.分布式表达(Distribute Representation)。通过激活跨越一组处理元件的模型进行存储记忆，而且存储是三相重叠的，在同一组处理元件上以不同的模拟方式，表示不同的记忆。

**2.分布异步控制(Distributed，Asynchronous Control)。**每个处理元件的功能是根据它自身的状态来作判断。所有局部作用相加就是整体的解决方法。

**3.相关存储器(Content-Addressable Memory)。**一个模型在网络中可以进行存储。如果我们想要跟踪一个模型，只需要确定其中一部分，那么网络就会自动找到相适应的匹配。

**4.容错(Fault Tolerance)。**如果有少数处理单元不起作用或出故障，那么网络的功能还能发挥作用。4

作用霍普菲尔德网络不仅数学处理非常精致，而且网络提出两年后，霍普菲尔德就设计出模拟该网络性质的电子线路，为模型的应用提供了成功的范例。最有名的就是运用霍普菲尔德网络解决NP难解问题中的典型问题——旅行商问题，结果在很短的时间内，网络就提供了满意的答案。佩尔顿(Pelton，M．)把这一问题看作是最优化问题。

霍普菲尔德网络是具有一定规模和灵活联结关系的多层神经网络，在刻画网络的整体状态时，霍普菲尔德指出网络状态的连续变化过程其实就是能量极小化的过程，当联结权重对称时系统就处于某种稳定状态，这就为网络动力学的稳定性提供了证据。由于他把稳定平衡点与正确的储存状态相对应，从而为联想储存提供了明确的物理解释。这种网络从系统功能角度出发，强调神经元的集体功能，初步显示了按内容寻址的联想记忆的性质。这一切均表明霍普菲尔德网络对人脑的模拟研究更加接近真实生物脑的情况，但它与生物脑之间的差距仍然是当代科学无法跨越的。因为，尽管人脑是由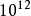 个神经元构成的，但单个神经元之间的关系却并不是随机的，神经元的位置和作用，不仅由千万年进化的系统发生决定，而且还由每个人出生后十多年的个体发育决定，所以脑内神经元的相互关系并不像固体物理自旋玻璃那样，是吸引子随机相互作用的相空间。生物脑的能量变化并不像淬火模型那样达到能量最小的稳定状态而收敛；相反，脑的能量代谢是有源的，从较小能量平衡态到全系统高能不平衡态，或达到某一局部最高能态时，才得到解。2

局限性霍普菲尔德网络虽然能实现联想记忆功能，但由于其记忆内容不可改变，因而不具备学习能力。而且这种网络能够正确记忆和回顾的样本数是相当有限的。如果记忆的样本数太多，网络可能收敛于一个不同于所有记忆中样本的伪模式；如果记忆中某一样本的某些分量与别的记忆样本的对应分量相同时，这个记忆样本可能是一个不稳定的平衡点。而且当网络规模一定时，所能记忆的模式非常有限。一般情况下，我们把网络所能储存的最大模式数称为网络容量，网络容量与网络的规模、算法以及记忆模式的向量分布都有关系。随着记忆模式数的增加，权值不断移动，各记忆模式相互交叉，当模式数超过网络容量时，网络不但逐渐遗忘以前记忆的模式，而且也无法记住新模式，这就说明当网络规模一定时，要记忆的模式数越多，联想时出错的可能性越大；反之，要求的出错概率越低，网络的信息储存容量的上限就越小。2