[科普中国]-样本相关系数

简介

样本是借助于特殊方法抽出而组成总体的一部分。样本的主要特点是： 它代表总体；它的容量小于总体容量。样本相关系数是指样本中变量之间的线性相关程度。样本相关系数准确性与很多因素都有关，如抽样方法，样本的容量。样本相关系数的计算公式如下：

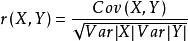其中Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差。r的取值范围为-1≤r≤1，当r接近±1时表明观察的数据线性相关较强，当r接近0时表明观察数据无线性相关。当用样本相关系数来反映总体的变量之间是否相关，在样本容量比较小时通常需要进行相关系数的检验。

抽样方法在统计学中，抽样（Sampling）是一种推论统计方法，它是指从目标总体（Population，）中抽取一部分个体作为样本（Sample），通过观察样本的某一或某些属性，依据所获得的数据对总体的数量特征得出具有一定可靠性的估计判断，从而达到对总体的认识。

简单随机抽样（simple random sampling），也叫纯随机抽样。从总体N个单位中随机地抽取n个单位作为样本，使得每一个容量为样本都有相同的概率被抽中。特点是：每个样本单位被抽中的概率相等，样本的每个单位完全独立，彼此间无一定的关联性和排斥性。简单随机抽样是其它各种抽样形式的基础。通常只是在总体单位之间差异程度较小和数目较少时，才采用这种方法[1]。

系统抽样（systematic sampling），也称等距抽样。将总体中的所有单位按一定顺序排列，在规定的范围内随机地抽取一个单位作为初始单位，然后按事先规定好的规则确定其他样本单位。先从数字1到k之间随机抽取一个数字r作为初始单位，以后依次取r+k、r+2k……等单位。这种方法操作简便，可提高估计的精度。

分层抽样（stratified sampling）。将抽样单位按某种特征或某种规则划分为不同的层，然后从不同的层中独立、随机地抽取样本。从而保证样本的结构与总体的结构比较相近，从而提高估计的精度。

整群抽样（cluster sampling）。将总体中若干个单位合并为组，抽样时直接抽取群，然后对中选群中的所有单位全部实施调查。抽样时只需群的抽样框，可简化工作量，缺点是估计的精度较差1。

相关系数相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。

简单相关系数：又叫相关系数或线性相关系数，一般用字母P 表示，是用来度量变量间的线性关系的量。

复相关系数：又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如，某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。

典型相关系数：是先对原来各组变量进行主成分分析，得到新的线性关系的综合指标，再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。

数据分布的敏感度存在性总体皮尔逊相关系数被定义成矩，因此任意的双变量概率分布是非零的，也就是说总体协方差和边缘总体方差是由定义的。一些概率分布，诸如柯西分布有未定义的方差，因此X or Y 如果服从这种分布，ρ便是未定义的。在实际应用中，如果有数据被怀疑服从重尾分布，这个条件就需要引起重视。然而，相关系数的存在性通常并需要太介意；例如，如果分布是有界的，ρ便总是有意义的。

大样本的特性在双变量正态分布的案例中，只要边缘均值和方差是已知的，总体相关系数描述的是便是联合分布。在其他的双变量分布中，这个结论并不正确。总之，不论两个随机变量的联合分布是不是正态的，相关系数在研究的它们之间的线性依赖性都是有帮助的。样本相关系数是对两个正态分布变量总体相关系数的最大似然估计并且是渐进无偏的和有效的，这也就是说如果数据是正态的并且样本容量是中等的或大量的，就不可能构造出一个比样本相关系数更准确的估计。对于非正态的数据，样本相关系数大致上是无偏的，但有可能是无效的。只要样本均值、方差和协方差是一致的（当大数定理可以应用的情况下），样本相关系数是总体相关系数的 一致估计 。

稳健性与其他常用的统计指标相似的，样本指标r不是稳健的。因此如果由异常值，这个指标是有误导性的。特别的，PMCC 既不是稳健分布的，也不是异常值稳健的)。对X 和 Y的散点图的观察可以很明显的揭示出缺乏稳健性的情况，在这种情况下，采用的联合的方法是比较明智的。注意到，虽然大多数稳健的估计器从某种程度上说都是有统计依赖的，它们总的来说，在总体相关系数的尺度上都是可辨的。

基于皮尔逊相关系数的统计推断对数据分布式敏感的。 如果数据大致是正态分布的，可以使用精确检验和基于Fisher变换的渐进检验，但是它们可能由误导性。 在一些情况下，自助采样可以用来构造置信区间。 同时， 重复抽样 可以应用在假设检验中。 这些非参数化 的方法在某些情况下，如双变量正态分布不能保证时，可能得出更有意义的结论。然而，这些方法的标准形式依赖于数据的 可交换性。这也就意味着被分析的数据时没有顺序的和组别的。因为这有可能会影响估计相关系数的特性。

分层分析是一种容许缺少双变量正态性的方法，或者说是用来隔离相互关联因素的关联结果。 如果W代表聚类成员或者其它需要被控制的因素，我们可以分离基于W的数据, 然后我们可以再每个层里计算相关系数。 当我们控制变量W，我们便能在层的等级上估计与所有相关系数相关的各自的相关系数。