[科普中国]-半迭代法

迭代法

迭代是数值分析中通过从一个初始估计出发寻找一系列近似解来解决问题（一般是解方程或者方程组）的过程，为实现这一过程所使用的方法统称为迭代法（Iterative Method）。

一般可以做如下定义：

对于给定的线性方程组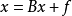 （这里的x、B、f 同为矩阵，任意线性方程组都可以变换成此形式），用公式 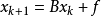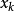（ 代表迭代k 次得到的x，初始时k=0)逐步带入求近似解的方法称为迭代法（或称一阶定常迭代法）。如果 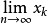存在，记为x*，称此迭代法收敛。显然x*就是此方程组的解，否则称为迭代法发散。

跟迭代法相对应的是直接法（或者称为一次解法），即一次性的快速解决问题，例如通过开方解决方程x +3= 4。一般如果可能，直接解法总是优先考虑的。但当遇到复杂问题时，特别是在未知量很多，方程为非线性时，我们无法找到直接解法（例如五次以及更高次的代数方程没有解析解，参见阿贝耳定理），这时候或许可以通过迭代法寻求方程（组）的近似解。

最常见的迭代法是牛顿法。其他还包括最速下降法、共轭迭代法、变尺度迭代法、最小二乘法、线性规划、非线性规划、单纯型法、惩罚函数法、斜率投影法、遗传算法、模拟退火等等。

半迭代法的发展考虑线性方程组

A x = b (1)

其中 A 是 n 阶大规模稀疏非奇异实矩阵。由于存储量和运算量等原因，解决这一类问题的常用方法是迭代方法。迭代法因算法灵活，程序易于实现等原因，已成为求解大规模稀疏线性方程组三大类方法之一 1。然而迭代法的收敛性、收敛速度以及它的健壮性等是制约迭代方法有效使用的三大要素。为了使迭代法更加实用有效，对迭代法加速是十分必要的。在众多的加速方法中，1962年提出的半迭代法(Semi-iterative method)是对迭代法进行加速的一种非常有效的方法，在实际使用中效果非常理想。

研究表明，如果迭代矩阵可对角化，只要迭代矩阵的特征值分布密集 ，则半迭代法加速效果非常理想。而如果迭代矩阵的最大特征值接近 1 时，直接采用半迭代加速效果不会太理想。

若干记号和引理设 n 阶矩阵G有 M个相异实特征值，按模排列为

0