[科普中国]-BCH循环码

概述

若循环码的生成多项式具有如下形式： g(x)=LCM[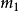(x),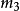(x),…,(x)] 其中LCM表示最小公倍式，t为纠错个数，(x)为素多项式，则由此生成的循环码称为BCH循环码，其最小码距d≥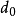=2t+1(d0称为设计码距)，它能纠正t个随机独立差错。

循环码具有某种循环特性的线性分组码，如果(n，κ)线性分组码Vκ具有如下的性质：对于每一个A=(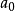,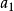，…，)∈Vn，只要∈Vκ，其循环移位亦属于Vκ，则称Vκ为循环码。循环码的优点在于其编码和译码手续比一般线性码简单，因而易于在设备上实现。使Vn中的每一个矢量A=(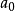,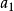，…，)，对应于域GF上的多项式ɑ(x)=ɑ0+ɑ1x+…+x。于是Vn中的全体n维矢量便与上述多项式之间建立了一一对应的关系。基于这种对应，使Vn中除了线性运算而外，还建立了矢量之间的乘法运算。A=(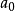,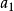，…，)与B=(b0,b1,…,)的乘积ab可视为ɑ(x)b(x)[mod(x-1)]所对应的矢量。因此,一个(n,κ)循环码的生成矩阵及均等校验矩阵可分别由生成多项式及均等校验多项式h(x)所代替，从而简化了编码及译码运算。

计算公式设计距离为9的q元BCH码的周期分布的计算公式：码的周期分布为q的幂，当码的周期不等于某些特殊值时，幂为码长与周期的最大公因数。当码的周期为特殊值时，幂为n/b-m[8/b]，这里n是码的长度，b是由n和码的周期决定的2到8之间的整数，m是q模n的指数。由此计算公式和Mobius反转公式给出了无内周期码字个数的计数结果。1

基本原理BCH码是一种有限域中的线性分组码，具有纠正多个随机错误的能力，通常用于通信和存储领域中的纠错编码。BCH码定义如下：给定任意一个有限域GF(q)及其扩展域GF(q^m)，其中q是素数或素数的幂，m为正整数。对于任意一个码元取自扩展域GF(q^m)的循环码(n,k)，其中n=2^m-1，其生成多项式g(x)具有2t个连续的根{a^1,a^2,a^,...,a^(2t-1),a^(2t)}，则由生成多项式g(x)编码产生的循环码称为q进制的BCH码，记为(n,k,t)。当码长n=2^m-1，称为本原BCH码，否则称为非本原BCH码。

最常用的BCH码是二进制的BCH码。二进制BCH码的所有码元都是由0和1构成，便于硬件电路的实现。如无说明，本文以下讨论的BCH码都是二进制BCH码。二进制本原BCH码具有以下重要参数：

码长：n=2^m-1

校验位长度：n-k