[科普中国]-雷诺平均方程

计算机性能的飞速提升和流体力学数值计算方法的迅速发展，为计算流体力学(CFD)的发展提供了必要的前提条件，从而奠定了计算流体力学(CFD)在国民经济中的重要地位。计算流体力学已经发展成为“解决气象、交通、建筑、桥梁和生命科学等多领域中流体力学问题”的强有力工具。尤其在航空、航天领域，计算空气动力学已经与实验空气动力学一起被视作空气动力学两大并列的分支，它们互相补充，互相验证，共同发展进步。计算流体力学是多领域交叉的综合性学科，涉及计算机科学、流体动力学、偏微分方程的数学理论、计算几何、数值分析等多方面;这些学科交又融合，相互促进和支持，又推动了这些学科的深入发展。

在近三十年来，随着速势方法、求解Euler方程方法以及Euler方程与附面层方程耦合迭代方法等数值求解技术的不断发展和完善，计算流体力学己经可以像实验一样十分逼真地模拟真实的流动过程，从而部分取代了实验研究，在工程应用领域中有着不可替代的作用。然而对于某些复杂的粘性绕流，如强激波/附面层相互干扰、大迎角分离流动、旋涡的形成与发展等问题，上述方法则显得力不从心，所以人们逐步发展了Navier-Stokes困S)方程的数值求解技术。以前由于受到计算机的限制，对复杂外形的粘性绕流的NS方程求解，发展相对缓慢。在近几年时间里，得益于计算机技术的发展，已经可以利用计算机求解NS方程，模拟复杂外形飞行器的粘性绕流。

现代飞行器设计要求我们采用的数值方法尽可能精确的模拟流场的粘性效应，以准确地预测各种外形飞行器的气动力特性。引入湍流模型计算雷诺平均的NS方程(RANS)，是目前数值模拟复杂粘性流场的主要方法，加入湍流模型后的RANS方程在计算升力、阻力、力矩方面的精度能得到极大提高。

湍流是流体的一种流动状态。当流速很小时，流体分层流动，互不混合，称为层流，也称为稳流或片流；逐渐增加流速，流体的流线开始出现波浪状的摆动，摆动的频率及振幅随流速的增加而增加，此种流况称为过渡流；当流速增加到很大时，流线不再清楚可辨，流场中有许多小漩涡，层流被破坏，相邻流层间不但有滑动，还有混合,形成湍流，又称为乱流、扰流或紊流。

在自然界中，我们常遇到流体作湍流，如江河急流、空气流动、烟囱排烟等都是湍流。

湍流是在大雷诺数下发生的，雷诺数较小时，黏滞力对流场的影响大于惯性力，流场中流速的扰动会因黏滞力而衰减，流体流动稳定，为层流；反之，若雷诺数较大时，惯性力对流场的影响大于黏滞力，流体流动较不稳定，流速的微小变化容易发展、增强，形成紊乱、不规则的湍流流场。

湍流基本特征是流体微团运动的随机性。湍流微团不仅有横向脉动，而且有相对于流体总运动的反向运动，因而流体微团的轨迹极其紊乱，随时间变化很快。湍流中最重要的现象是由这种随机运动引起的动量、热量和质量的传递，其传递速率比层流高好几个数量级。

雷诺平均方程是描述湍流统计量的演化的系综平均N-S方程。1

纳维-斯托克斯方程(英文名;Navier-Stokes equations)，描述粘性不可压缩流体动量守恒的运动方程。简称N-S方程。粘性流体的运动方程首先由Navier在1827年提出，只考虑了不可压缩流体的流动。Poisson在1831年提出可压缩流体的运动方程。Saint-Venant在1845年，Stokes在1845年独立提出粘性系数为一常数的形式，现在都称为Navier-Stokes方程，简称N-S方程。在直角坐标系中，其矢量形式为=-Ñp+ρF+μΔv。

纳维-斯托克斯方程(Navier-Stokes equation)描述粘性不可压缩流体动量守恒的运动方程，简称N-S方程。此方程是法国科学家C.-L.-M.-H.纳维于1821年和英国物里学家G.G.斯托克斯于1845年分别建立的，故名。

雷诺平均NS 方程是流场平均变量的控制方程，其相关的模拟理论被称为湍流模式理论。湍流模式理论假定湍流中的流场变量由一个时均量和一个脉动量组成，以此观点处理NS 方程可以得出雷诺平均NS 方程（简称RANS 方程）。再引入Boussinesq 假设，即认为湍流雷诺应力与应变成正比之后，湍流计算就归结为对雷诺应力与应变之间的比例系数（即湍流粘性系数）的计算。正是由于将控制方程进行了统计平均，使得其无需计算各尺度的湍流脉动，只需计算出平均运动，从而降低了空间与时间分辨率，减少计算工作量。根据计算中使用的变量数目和方程数目的不同，湍流模式理论中所包含的湍流模型又被分为二方程模型、一方程模型和零方程模型（代数模型）等大类。FLUENT 中使用的三种k −ε模型、Spalart-Allmaras 模型、k −ω模型及雷诺应力模型（RSM）等都属于湍流模式理论。雷诺平均模型的主要缺点是它只能提供湍流的平均信息，这对于近代自然环境的预报和工程设计是远远不够的；雷诺平均模型的致命弱点是它的模型没有普适性。

空气的可压缩RANS方程可以写成采用求和约定的笛卡儿张量形式。

连续方程：

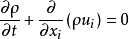
动量方程：

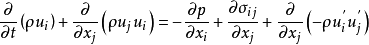
其中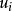 表示略去平均符号的雷诺平均速度分量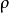， 为密度，p为压强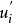， 为脉动速度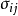， 为应力张量分量。2

预测湍流的统计量的湍流统计理论或其他基础研究在近期内还看不到突破的希望，受计算机水平的限制，从NS方程出发对湍流进行直接数值模拟(DNS)，难以解决工程中遇到的复杂湍流问题，依靠实验取得经验数据，不仅耗资巨大，周期很长，而且对于某些实际工程问题，完全相似的实验室模拟不可能实现。在这种情况下，求解雷诺平均的NS方程(RANS)方法成为解决工程问题比较有效、切实可行的手段。

但RANS方法也有它的缺陷:在平均运动中湍流脉动量的影响即雷诺应力是未知的，需要建立湍流模型。所谓湍流模型，就是以雷诺平均NS(RANS)方程与脉动方程为基础，依靠理论与经验的结合，引进一系列模型假设，建立一组描写湍流平均量的封闭方程组的理论计算方法。雷诺应力的主要贡献来自大尺度脉动，而大尺度脉动的性质及结果和流动的边界条件密切相关，因此雷诺应力的封闭模型不可能是普适的，就是说，不存在对一切复杂流动都适用的统一封闭模型。3