采用贝叶斯决策,需要对概率分布进行估计,然后通过最大似然或者贝叶斯估计的方法估计其分布的参数,然后在通过贝叶斯分类器进行分类,这种方法叫做参数判别方法。
然而实际上,对样本分布的估计往往是不准确的,也是比较困难的。针对不同的情况,设计不同的分类器,这种方法不通过分布假设、参数估计,而是根据样本信息直接设计分类器,这种方法叫做非参数判别方法。
线性分类器设样本d在维特征空间中描述,则两类别问题中线性判别函数的一般形式可表示成
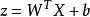 其中,
其中,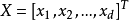 ,
,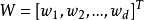 ,b是阈值,常数。
,b是阈值,常数。
以二分类任务为例,将输出标记为 ,而
,而 是实值,于是将实值
是实值,于是将实值 转化为
转化为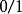 值,最理想的是“单位阶跃函数”:
值,最理想的是“单位阶跃函数”:
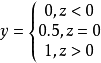 相应的决策规则可表示成:
相应的决策规则可表示成:
若预测值z大于零,判为正例;
若预测值z小于零,判为反例;
若预测值z为临界值零,可判为任意。1
线性判别分析线性判别分析(Linear Discriminant Analysis,简称LDA)是一种经典的线性学习方法,在二分类问题上因为最早由Fisher提出,亦称“Fisher判别分析”。
LDA的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、异类样本尽可能远离;在对新样本进行分类时,将其投影到同样的这条直线上,再根据其投影点的位置来确定新样本的类别。
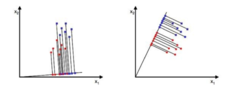
从直观上来看,右图比较好,可以很好地将不同类别的样本点分离。接下来我们从定量的角度来找到这个最佳的w。首先我们寻找每类样例的均值(中心点),这里i只有两个
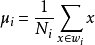 由于x到w投影后的样本点均值为
由于x到w投影后的样本点均值为
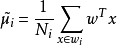
由此可知,投影后的的均值也就是样本中心点的投影。
什么是最佳的直线(w)呢?
同类样例的投影点尽可能接近、异类样本尽可能远离的直线就是好的直线。
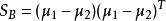
对投影后的类求散列值(scatter),如下:
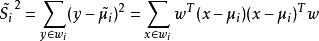 定义
定义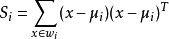
定义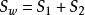 ,
,
则J(w)最终可以表示为:
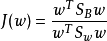
上式即为LDA欲最大化的目标,即 和
和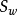 的“广义瑞利商”。
的“广义瑞利商”。
决策规则:
在对新样本进行分类时,将其投影到同样的这条直线上,再根据其投影点的位置来确定新样本的类别。
感知器感知机学习旨在求出将训练数据集进行线性划分的分类超平面,为此,导入了基于误分类的损失函数,然后利用梯度下降法对损失函数进行极小化,从而求出感知机模型。感知机模型是神经网络和支持向量机的基础。
感知机模型如下:
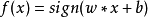 其中,x为输入向量,sign为符号函数,括号里面大于等于0,则其值为1,括号里面小于0,则其值为-1。w为权值向量,b为偏置。
其中,x为输入向量,sign为符号函数,括号里面大于等于0,则其值为1,括号里面小于0,则其值为-1。w为权值向量,b为偏置。
求感知机模型即求模型参数w和b。
感知机预测,即通过学习得到的感知机模型,对于新的输入实例给出其对应的输出类别1或者-1。
与线性分类器类似。
支持向量机支持向量机(Support Vector Machine,SVM)是Corinna Cortes和Vapnik等于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。在机器学习中,支持向量机(SVM,还支持矢量网络)是与相关的学习算法有关的监督学习模型,可以分析数据,识别模式,用于分类和回归分析。
给定训练样本集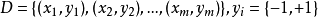 ,分类学习的基本思想时:基于数据集D再样本空间中找到一个超平面,将不同类别的样本分开,但能找到的这个超平面可能有很多,如何去确定哪一个最好呢?
,分类学习的基本思想时:基于数据集D再样本空间中找到一个超平面,将不同类别的样本分开,但能找到的这个超平面可能有很多,如何去确定哪一个最好呢?

直观上来看,应该寻找位于两个训练样本“正中间:的划分超平面,即图2中红色的那个,因为该超平面对训练样本的局部扰动的”容忍“性最好。在样本空间中,划分超平面可通过如下线性方程来描述:
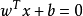
样本空间任意点x到超平面 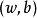 的距离可写为:
的距离可写为:
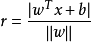
假设超平面能将训练样本正确分类,即,对于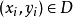 ,若
,若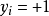 ,则有
,则有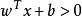 ;若
;若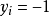 ,则有
,则有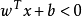 。
。
距离超平面最近的几个点被称为”支持向量“,两个异类支持向量到超平面的距离之和为:
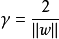
它被称为“间隔”
欲找到具有最大间隔的划分超平面,也就是要满足以下条件:
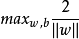
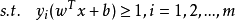
决策规则:
在对新样本 进行预测分类时,计算
进行预测分类时,计算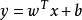 ,若y>0,则预测为正例;若y
,若y>0,则预测为正例;若y




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国