[科普中国]-十六进制至十进制转换

进制转换是人们利用符号来计数的方法。进制转换由一组数码符号和两个基本因素“基数”与“位权”构成。基数是指，进位计数制中所采用的数码（数制中用来表示“量”的符号）的个数。位权是指，进位制中每一固定位置对应的单位值。

十进制中的数位排列是这样的…… 万 千 百 十 个 十分 百分 千分……

16进制中的数位排列是这样的…… ……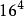

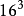
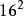
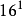
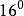
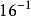
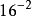
对于整数部分，用被除数反复除以16，除第一次外，每次除以16均取前一次商的整数部分作被除数并依次记下每次的余数。另外，所得到的商的最后一位余数是所求二进制数的最高位。

对于小数部分，采用连续乘以基数16，并依次取出的整数部分，直至结果的小数部分为0为止。故该法称“乘基取整法”。

给你一个十进制，比如：120，如何将它转换成十六进制数呢？

10进制数转换成十六进制数，这是一个连续除以16的过程：把要转换的数，除以16，得到商和余数，将商继续除以16，直到商为0。最后将所有余数倒序排列，得到数就是转换结果。

比如要转换120为十六进制数：

“把要转换的数，除以16，得到商和余数”，那么：要转换的数是120， 120 ÷ 16，得到商是7，余数是8。

“将商继续除以16,直到商为0……”，现在商是7，还不是0，所以继续除以16。

那就： 7 ÷ 16, 得到商是0,余数是7。现在商已经是0。

我们两次计算依次得到余数分别是：8、7，将所有余数倒序排列，那就是：78。

故120转换成十六进制，结果是78。

把上面的一段改成用表格来表示，则为：

120转换为16进制，结果为：78。

16进制就是逢16进1，但我们只有0~9这十个数字，所以我们用A，B，C，D，E，F这六个字母来分别表示10，11，12，13，14，15。字母不区分大小写。

十六进制数的第0位的权值为16的0次方，第1位的权值为16的1次方，第2位的权值为16的2次方……

所以，在第N（N从0开始）位上，如果是是数 X （X 大于等于0，并且X小于等于 15，即：F）表示的大小为 X * 16的N次方。

假设有一个十六进数 2AF5, 那么如何换算成10进制？

用竖式计算：

2AF5换算成10进制:

第0位：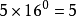

第1位：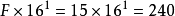

第2位：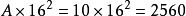

第3位：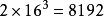

直接计算就是：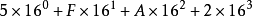

可以看出，所有进制换算成10进制，关键在于各自的权值不同。1