[科普中国]-数据流分析

数据流分析是一项编译时使用的技术，它能从程序代码中收集程序的语义信息，并通过代数的方法在编译时确定变量的定义和使用。通过数据流分析，可以不必实际运行程序就能够发现程序运行时的行为，这样可以帮助大家理解程序。数据流分析被用于解决编译优化、程序验证、调试、测试、并行、向量化和片行编程环境等问题。1

理解数据流分析的一个预备概念是控制流图（control flow graph，简称CFG），简而言之就是流图。CFG是一个有向图，它包含一部分程序的控制流。CFG典型的应用是代表类似过程大小的程序片断。1

典型的流图结点是基本块(总是顺序执行的代码片断)，流图的边代表基本块之间可能存在的控制流，其中的一个结点被标明为开始。

控制流分析跟踪程序可能执行的路径，数据流分析沿着可能的控制流路径跟踪数据可能的定义和使用，并收集有关特定数据项属性的信息。从根本上来说，数据流分析的目的是确定路径谓词的真或假。路径谓词是一些语句，这些语句表示在程序执行当中沿着一定的控制流路径发生了什么，在所有这些路径上使用任意或存在量词对语句进行量化。路径的定义与CFG有关，一条控制流路经是在CFG中的一条路径。1

数据流分析包括过程内的和过程间的数据流分析。常见的过程内数据流问题包括：到达定值，活跃使用，可用表达式和频繁使用，可用表达式和频繁使用。过程间数据流问题包括：形式边界集合，可能别名和可能被修改。另外，过程内的数据流问题在过程间数据流分析中也会出现。

目前出现的许多数据流算法可以被归类为：迭代算法，消除算法，及可达性算法。

选代算法通过初始化节点变量为一些可靠的值，并且连续地计算这些变量值，直到到达一个固定点，来解决等式系统。对于round robin版本的迭代算法是重复计算所有节点的数据流属性，直到属性值稳定。如果位向量的大小是r，计算复杂度为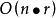。这样，最坏情况下在图上可能有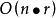次迭代，每次迭代涉及n个节点属性的计算。如果所有的r位能够一步被处理，复杂性就变成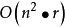。在单向问题中数据流只朝着一个方向，节点被后序遍历还是逆后序遍历依数据流的方向而定。这样d+2次迭代就足够了，这里d是流图深度的6次方，因此复杂性是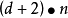。1

对于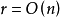的程序，所有的r位向量不能被一步处理，而处理一个r位的位向量本身将需要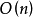步，因此迭代方法的复杂度的上下界分别为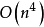和。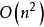

消除算法通过利用流图的结构属性减少解决数据沉问题所需要的大量工作。通过连续的应用图的转换使流图归约到一个点，图的转换就是使用图的分析或图的分裂去分析区间以获得一个派生图。在一个区间内，数据流的属性是由区间内头节点的数据流的属性来确定的。这样可以延迟替代联立方程中的些值。对于单向流问题，这些方法典型的复杂度为O(N)，这里N是在归约图序列中节点的总数。尽管它们已经被用于解决一类受限制的双向问题，但消除算法不能被扩展到一般的双向数据流问题。1

可达性算法是由哥本哈根大学的Thomas Reps及Mooly Sagiv等人在1994年提出来的。可达性算法把过程问数据流问题转换成一种特殊的图形可达性问题(可达性是指沿着过程问间可实现路径)，然后解决通过有效的图的算法。该算法的局限在于数据流实际匕是一个有限的集合，并且数据流函数分布在集合操作(并或交)上。1

该算法解决了一大类过程间的数据流分析问题，从时间复杂度来看，它是多项式时间算法。1

数据流信息的计算非常复杂，尤其是过程问数据流分析，由于过程间的调用关系比较复杂，使得静态的数据流分析更为困难。然而在所有程序点计算完整的数据流信息并不总是必要的，所以文章提出了需求过程间数据流分析方法。该分析方法在很多方面比完全分析是更可取的。1

它能缩小感兴趣点的焦点：所使用的数据流分析软件工具经常需要的信息仅在某些特定的程序点的集合。在程序的优化阶段，尽管转换可以被组织在一些热点，但在早期阶段需要使用完全数据流分析确定数据流事实。需求算法可以大量地减少需要计算的外部信息。

它能缩小感兴趣的专门的数据流事实的焦点：尽管在每个程序点P数据流信息是需要的，但在P点的整个数据流的集合是不需要的。

减少初步阶段的工作：在那些能被分成独立阶段的问题中，并非上一阶段所有的信息对下一阶段束说都是必要的。需求算法可以减少花费在准备阶段或其他辅助阶段的大量工作。

需求分析作为一个用户级的操作：人们希望有一个程序开发工具，用户能够向它交互地提问关于程序各个方面的问题。当要理解复杂的代码时这种工具是非常有用的。

需求过程间数据流分析方法的主要思想是：仅为感兴趣的单个程序元素(或少数感兴趣的元素)报告扼要信息(summalyinformation)。因为在一个程序点的扼要信息决定于在其他点的扼要信息，在这些点上需要计算其扼要信息(或者计算其信息的数量)，所以最重要的就是最小化其他点的数目。

从该思想出发，把获得需求算法分为两个阶段：1

(1) 把过程间数据流的完全算法编码成一个逻辑程序；

(2) 通过应用一个转换-称为Alexander方法或魔术集合转换，把完全算法转换为一个需求算法。

以Sharir和Pnueli的过程间的“函数方法”为基础进行了验证，结果证明该方法是实际可行的。

数据流分析技术对于分析程序行为来说是一项有力的技术。然而，大量的工作都是相对于顺序化的程序做的，对并发程序的数据流分析的工作很少。因此，数据流技术今后的发展除了要研究出更有效、更准确、更快速的算法外，还要开发出引对并发程序的数据流分析技术。1