[科普中国]-状态反馈控制

控制系统最基本的结构形式是由受控系统和实现反馈控制规律的反馈环节所构成的反馈控制制系统。在古典控制理论中，反馈信号一般取自输出信号，反馈形式为输出反馈，而在现代控制理论中，基本反馈形式就是状态反馈。状态反馈是将系统的何一个状态按照一定的比例反馈到输入端，与系统的参考输入进行综合形成控制律，作为受控系统的控制输入。

状态反馈控制是现代控制理论的一种特色。 一个系统的状态变量可以展现其整个系统的内部特性而不需要知道系统的内部结构。 所以相对于传统的输出反馈控制， 状态反馈控制能够更优秀更有效的控制系统， 使其稳定正常工作。 然而由于状态变量是不能直接由系统外部直接测量得到的， 这让状态反馈技术在实现的过程中相对于输出反馈复杂。状态反馈变量不会影响原系统的能控性， 但是可能会改变系统的能观性只要原系统是能控的， 则一定能够通过选着适当的反馈增益矩阵 K 用状态反馈来任意移植闭环系统的极点。这一点传统的输出反馈控制是不能做到的。

状态反馈控制的定义为：将系统的每一状态变量乘以相应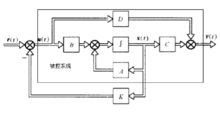的反馈系数， 反馈到输入端, 与参考输入相加，其和作为被控系统的控制信号。

状态反馈控制系统的基本结构如图1所示，其中虚线框内是被控系统，矩阵K为反馈矩阵，反馈矩阵K起主要作用。

设系统的状态空间表达式为：

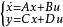
设状态反馈矩阵 为该系统的状态反馈增益矩阵，在一般情况下，控制规律是参考输入向量r(t)及状态向量x(t)的非线性函数，即：u(t)=f(r(t)，x(t))。对于线性定常系统，可以把控制向量u(t)视为向量r(t)及x(t)的线性函数，即：u(t)=r(t)-Kx(t)。将上式代入被控控系统的状态方程：dX(t)/dt=(A-BK)X(t)-Br(t)，从而状态反馈系统的传递函数矩阵为：

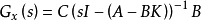
系统在未实行状态反馈时的传递函数知阵为：

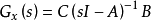
可见，状态反馈矩阵K的引入，没有增加系统的维数。可以得到闭环系统矩阵为 ( A-BK)，再由系统特征多项式可以看出，再加入|λI-(A-BK)|可以看出，再加入状态反馈矩阵以后，系统矩阵和特征值有所改变，但是其 A、B 值均无变化。因此，可以通过矩阵K的选择来改变系统的特征值(即改变系统的极点)，从而可使系统获得期望的性能。

系统的可控性和可观性是Kalman在1960年首先提出来的，它是状态反馈控制、最优控制和最优控制的基础。状态空间表达式揭示了系统内部运动的状态里与外部输入输出量之间的关系。

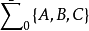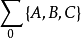定理：多变量线性系统（定常的或时变的） ，在任何形如u(t)=r(t)+K(t)x(t)的状态反馈下，这个状态反馈闭环系统 完全可控的充要条件是被控对象 完全可控。

该定理对于多变量时变系统也是合适的。

虽然状态反馈保持了动态方程的可控性，但总可以选择某一状态反馈阵 K，破坏动态方程的可观性。状态反馈不改变系统的可控性， 但可能改变系统的可观性。一般地说， 当用状态反馈配置的系统极点与原系统相同时， 即出现零、 极点对消时，状态反馈就改变了系统的可观性。

定理：输出反馈闭环系统可控的充要条件是被控系统可控； 输出反馈闭环系统可观的充要条件是被控系统可观。

极点配置定理：线性（连续或离散）多变量系统 {A,B,C} 能任意配置极点的充分必要条件是，该系统状态完全可控。

1) 期望闭环极点组的性能指标属性：期望闭环极点组具有二重性， 理论计算上的闭环期望极点组和控制工程中的直观性能指标。

2) 控制工程中基本类型的性能指标：时间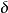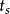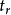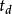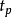域： 、 、 、 、 、 、ζ；频率域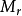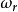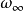： 、 、 ；它们间可以相互转化，如：

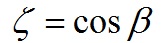
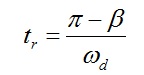
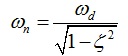
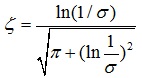
3) 基本类型性能指标和期望闭环极点组的主导极点对的关系：

4) 期望闭环极点组的确定主导极点：1

主导极点为：