[科普中国]-D分离

基本概念

在贝叶斯网络的学习过程中，经常会遇到D分离（D-Separation）这个概念，D分离是寻找网络节点之间的条件独立性的一种方法或者说一种问题的简化处理的技巧。采用D分离技术，在用贝叶斯网络进行预测，诊断推理等方面，可以提高计算速度，减少计算复杂性。

原理对于给定的结点集ε，如果对贝叶斯网中的结点Vi和Vj之间的每个无向路径，在路径上有某个结点Vb，如果有属性：

（1）Vb在ε中，且路径上的两条弧都以Vb为头（即弧在Vb处开始（出发））；

（2）Vb在ε中，路径上的一条弧以Vb为头，一条以Vb为尾 ；

（3）Vb和它的任何后继都不在ε中，路径上的两条弧都以Vb为头（即弧在Vb处结束）；

则称Vi和Vj 被Vb结点阻塞。

如果Vi和Vj被证据集合ε中的任意结点阻塞，则称Vi和Vj是被ε集合D分离，结点Vi和Vj条件独立于给定的证据集合ε，即P(Vi|Vj,ε) =P(Vi|ε)和P(Vj|Vi,ε) =P(Vj|ε)，表示为：I(Vi,Vj|ε) 或I(Vj,Vi|ε) 。

无向路径：DAG图是有向图，所以其中的路径也应该是有向路径，这里所指的无向路径是不考虑DAG图中的方向性时的路径。

条件独立：如具有以上三个属性之一，就说结点Vi和Vj条件独立于给定的结点集ε。

阻塞：给定证据集合ε，当上述条件中的任何一个满足时，就说Vb阻塞相应的那条路径。

D分离：如果Vi和Vj之间所有的路径被阻塞，就叫证据集合ε可以D分离Vi和Vj。D分离的实质就是寻找贝叶斯网中的条件独立语义，以简化推理计算。

三种情况独立分析情况一tail-to-tail

节点c连接的是两个箭头的尾部，如图：

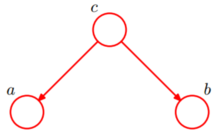
可知，P(a,b,c)=P(a|c)*P(b|c)*P(c)(1)

现在我们求P(a,b)，如果P(a,b)=P(a)*P(b)，则a和b是在c条件下独立分布的。分两种情况进行讨论：

（1）c值不作为观察点。令(1)式对c求积分，消去c值，考虑c是离散的情况，可得

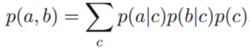
可以看到，与P(a,b)=P(a)*P(b)不等，所以a和b不是c条件独立的。

（2）c值作为观察点（即以c作为条件）。则可以知道c取某个c状态的概率为P(c)，c条件下a和b发生的概率为P(a,b|c)。由下式：

可得a和b是c条件下独立的。

情况二head-to-tail

可知，p(a,b,c)=p(a)*p(c|a)*p(b|c) (2)

同样分两种情况进行讨论：

（1）c值不作为观察点。对(2)式（考虑c是离散的情况）积分可得：

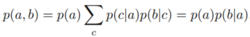
可知，a和b不是c条件独立的。

（2）c值作为观察点。则图模型表示为：

c条件下a和b发生的概率为P(a,b|c)。由下式：

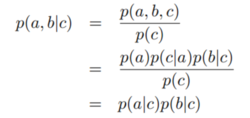
可知，a和b是c条件下独立的。

情况三head-to-head

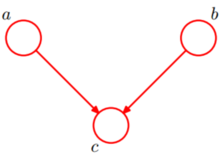
可知 p(a,b,c)=p(a)*p(b)*p(c|a,b) (3)

同理，分两种情况讨论：

（1）c值不作为观察点。由于所有p(c|a,b)相加和=1，所以有(3)式消去c，可得p(a,b)=p(a)*p(b)，即a与b是条件独立的。

（2）c值作为观察点。

所以有：

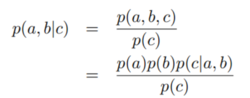
最后不能因式分解成p(a)*p(b)的形式，所以a与b不是c条件独立的。

基于D-Seperation的独立分析D-Separation是一种用来判断变量是否条件独立的图形化方法。相比于非图形化方法，D-Separation更加直观，且计算简单。对于一个DAG（有向无环图）E，D-Separation方法可以快速的判断出两个节点之间是否是条件独立的。

对于较为复杂的DAG图，我们可以给出一个普遍意义上的结论，也就是D-Seperation。对于DAG图E，如果A，B，C是三个集合（可以是单独的节点或者是节点的集合），为了判断A和B是否是C条件独立的，我们考虑E中所有A和B之间的无向路径。对于其中的一条路径，如果她满足以下两个条件中的任意一条，则称这条路径是阻塞（block）的：

（1）路径中存在某个节点X是head-to-tial或者tail-to-tail节点（情况一和情况二），并且X是包含在C中的；

（2）路径中存在某个节点X是head-to-head节点（情况三），并且X或X的儿子是不包含在C中的；

如果A，B间所有的路径都是阻塞的，那么A，B就是关于C条件独立的；否则，A，B不是关于C条件独立的。

实例根据D-Seperation分隔定理，我们可以很容易的判断是否是条件独立的。

判断图中a，b是否是c条件独立的：

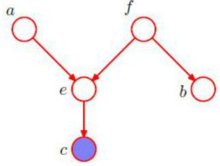
上图中a到b只有一条路径a->e->f->b。考虑路径上的点e和f，e是head-to-head类型的，且e的儿子节点就是c，根据（b），e是阻断的。所以a和b是c条件下独立的。

现在如果要判断a和b是否是f下条件独立的。同样的方法，考虑路径a->e->f->b上的所有节点。节点e是head-to-head类型的，e和她的儿子节点c都不在f中，所以e不是阻断路径的节点。节点f是tail-to-tail节点，且f就在f节点中，所以f节点阻断了路径。结论：a和b是f下条件独立的。

D-Seperation还可以用来证明独立同分布和马尔科夫边界等1。