概念
取左矢量(或右矢量)的一个集合,使任意左矢量(或右矢量)都能表示为它们的线性组合。这些左矢量(或右矢量)称为表象的基左矢(或基右矢)。基左矢和基右矢总称为基矢量。
在量子力学中,总是选一组完整的力学量的本征函数系所对应的左矢量(或右矢量)来作为基矢量。1
基本原理协变基矢量由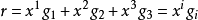 式求矢径对坐标的微分:
式求矢径对坐标的微分:
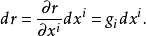 将矢径对坐标的偏导数定义为协变基矢量
将矢径对坐标的偏导数定义为协变基矢量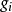 ,称为自然基矢量。即
,称为自然基矢量。即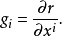 协变基矢量的方向沿坐标线正方向,其大小等于当坐标
协变基矢量的方向沿坐标线正方向,其大小等于当坐标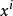 有1单位增量时两点之间的距离。因三个坐标线非共面,故
有1单位增量时两点之间的距离。因三个坐标线非共面,故
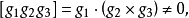 即
即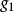 ,
,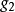 ,
, 线性无关。当
线性无关。当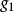 ,
,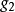 ,
, 构成左手系时,混合积为正值,记
构成左手系时,混合积为正值,记
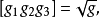 式中
式中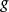 是一个正实数。
是一个正实数。
逆变基矢量定义一组3个与协变基矢量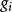 互为对偶的逆变基矢量
互为对偶的逆变基矢量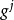 ,满足对偶条件:
,满足对偶条件:
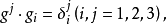 式中
式中 为三维的克罗内克尔
为三维的克罗内克尔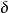 ,
,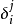 构成
构成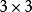 的单位矩阵。
的单位矩阵。
逆变基矢量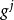 与协变基矢量的关系见图1示,
与协变基矢量的关系见图1示,
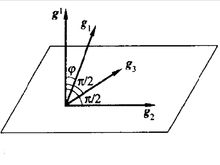
其方面垂直于另两个协定基矢量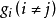 ,并与
,并与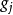 有夹角
有夹角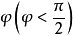 ,其模为
,其模为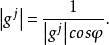
今后可以证明,逆变基矢量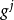 实际上是垂直于坐标
实际上是垂直于坐标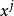 的等值面(即坐标面)的梯度。2
的等值面(即坐标面)的梯度。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国