[科普中国]-自校正控制系统

基本思想

自校正控制系统是一种把参数的在线辨识与控制器的在线设计有机结合在一起的控制系统，并在设计辨识算法和控制算法时考虑了随机干扰的影响，因此，属于随机自适应控制系统。自校正控制既能完成调节任务，也能承当伺服跟踪完成控制器的任务。它的基本思想是将参数估计递推算法与各种不同类型的控制算法结合起来，形成一个能自动校正控制器参数的实时的计算机控制系统。但是只有适当的辨识算法和合适的控制策略的结合才能产生既便于在线实施又具有稳定性的自校正控制算法。因此如何选择控制策略和辨识算法，如何将其有机地结合起来是自校正控制的关键问题之一。

确定性等价原理自校正控制系统通常属于随机适应控制系统，具有确定性等价性质，对于参数自适应的自校正控制系统来说，当所有的未知参数用它们的估计值代替后，其控制规律的形式与对应的参数已知时的随机最优控制规律的形式等价。因此，在确定自校正控制规律时，可根据确定性等价性质，先假定该系统的所有参数是已知的，并根据给定的性能指标综合出系统的最优控制规律，然后用估计模型来估计未知参数，并用估计结果代替上述最优控制律中的相应未知参数，就得到了自校正的控制规律。

需要注意的是，第一，确定性等价原理的前提是分离原理，也就是说，首先必须将参数和状态估计与控制分别考虑，然后才谈得上等价与否；第二，确定性等价原理的成立是有条件的，目前已经证明对于白噪声，可叠加的测量噪声和二次型性能指标的线性过程确定性等价原理是成立的。对于参数未知的随机情况，只有当参数是随机不相关时，确定性等价原理才成立。

自校正控制系统的结构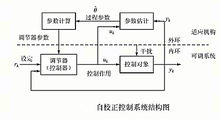自校正控制系统是由常规控制系统（内环）和自适应机构（外环）组成的，其中自适应机构包括递推参数估计器和控制参数计算器，其典型结构图如右图所示。1

参数估计器（辨识器）的作用是根据对象的输入输出信息，在线估计控制对象的参数θ，并将参数估计值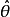 送到参数计算器。参数计算器则根据估计值计算控制器的参数。控制器再根据参数计算器的结果及事先选定的性能指标综合出相应的控制作用 uk ，使其能送出最优或次优的控制规律，保证系统运行的性能指标达到最优或接近最优状态。

系统开始运行时，由于参数估计值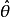 与其真值θ的差别可能很大，控制效果可能很差。但随着过程的进行，参数估计值会越来越精确，控制效果也会越来越好。当控制对象特性发生变化时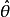， 会发生相应的改变，从而使控制器参数也发生相应的变化，自动适应了变化了的对象。因此尽管系统、环境在不断地变化，由于控制动作根据这些变化不断辨识，不断综合出新的控制率，因而系统具有一定的适应能力，能使性能趋于最优或次优，最终收敛到其参数已知时的最优控制。

自校正控制算法的分类从自校正控制算法所采用的控制策略来分类，自校正控制系统可以分为基于最优控制策略的自校正控制系统（如最小方差、广义最小方差自校正控制器），基于经典控制策略的自校正控制系统（如极点配置自校正调节器）和基于最优控制策略与经典控制策略相结合的自校正控制系统（如具有极点配置的广义自校正控制器）3类。

从自校正控制算法的实现方式来分类，有隐式（直接）算法和显式（间接）算法自校正控制算法两类。隐式算法是直接估计控制规律中的未知参数，显式算法则首先辨识被控系统的参数，然后将其估计值当成参数的真值去计算控制器的参数。在隐式算法中控制参数直接由过程参数估计值加以修改，所以隐式自校正采用的是预测控制原理，并且要求系统的延迟为已知的。在显式自校正中，过程参数的估计和控制规律的计算是分离的，因而过程参数的估计精度对于计算控制律是十分重要的。显式自校正是属于非直接控制的一类，其延迟可作为过程参数的一部分利用递推参数估计加以确定。隐式算法与显式算法比较由于省去了控制器设计计算这一步，从而可避免求解矩阵方程，使算法的鲁棒性有所提高。但当系统的延时较大时，显式算法则可减少辨识参数的个数，且容易将保证算法稳定的条件与被控系统的参数联系起来。

自校正控制的性能指标自校正控制技术的性能指标，根据控制对象的性质以及控制的目的和要求，可以有多种不同的结构形式。其中一种是误差二次型目标函数的形式，自校正控制策略用于保证这个二次型目标函数达到极小值，这种控制策略通常称为最小方差控制。自校正控制性能指标的另一种形式是在 20 世纪 70 年代中期和后期由Edmunds（1976）、Wellstead（1979）和 Astrom（1980）等人相继提出的，它不采用指标函数的形式，而是把预期的闭环系统的行为用一组期望传递函数的零极点的位置加以规定。自校正控制的策略就是保证实际的闭环系统的零极点收敛于这一组期望的零极点，这样的控制策略有时称为零极点配置的控制策略。2