[科普中国]-终结状态

简介

状态是对象执行某项活动或等待某个事件时的条件。转移是两个状态之间的关系，它由某个事件触发，然后执行特定的操作或评估并导致特定的结束状态。

状态图用于显示状态机（它指定对象所在的状态序列）、使对象达到这些状态的事件和条件、以及达到这些状态时所发生的操作。状态机由状态组成，各状态由转移链接在一起。状态图中可以有多种不同的状态，但有两种状态是不可或缺的，分别是起始状态和终结状态。起始状态是指一个活动或事件的开始。而终结状态代表一个活动或事件的结束。

进程的终结状态进程（Process）是计算机中的程序关于某数据集合上的一次运行活动，是系统进行资源分配和调度的基本单位，是操作系统结构的基础。在早期面向进程设计的计算机结构中，进程是程序的基本执行实体；在当代面向线程设计的计算机结构中，进程是线程的容器。程序是指令、数据及其组织形式的描述，进程是程序的实体。进程执行时的间断性，决定了进程可能具有多种状态。事实上，运行中的进程可能具有以下三种基本状态：就绪状态、运行状态(Running)、阻塞状态(Blocked)。在目前实际的系统中，为了管理的需要，还存在着两种比较常见的进程状态，即创建状态和终止状态。

终结状态：进程的终止也要通过两个步骤： 首先等待操作系统进行善后处理，然后将其 PCB 清零，并将 PCB 空间返还系统。当一个进程到达了自然结束点，或是出现了无法克服的错误，或是被操作系统所终结，或是被其他有终止权的进程所终结，它将进入终止状态。进入终止态的进程以后不能再执行，但在操作系统中依然保留一个记录，其中保存状态码和一些计时统计数据，供其它进程收集。一旦其它进程完成了对终止状态进程的信息提取之后，操作系统将删除该进程。1

自动机的终结状态有关概念计算机控制系统的控制程序具有有限状态自动机（FA）的特征，可以用有限状态机理论来描述。有限自动机（Finite Automata Machine）是计算机科学的重要基石，它在软件开发领域内通常被称作有限状态机（Finite State Machine），是一种应用非常广泛的软件设计模式。自动机是有限状态机(FSM)的数学模型。

自动机就是一个有内部状态的机器。它有一个初始状态，而每当它接收到一个字符，它就根据字符和当前的内部状态，更新自己的内部状态（新状态与旧状态和输入字符之间的函数关系称为状态转移函数），而当所有字符都处理完之后，我们根据自动机的最终状态，将接受的字符串分为两类：自动机接受的字符串和自动机不接受的字符串。

数学模型自动机可以表示为5-元组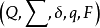 ，这里的：

Q 是状态的非空有穷集合。

∑ 是符号的有限集合，我们称为这个自动机接受的语言的字母表。 输入字符串都是∑上的字符串

δ 是状态转移函数，就是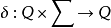 。(对于非确定自动机，空串是允许的输入)。

q0 是开始状态，就是说自动机在还未处理输入的时候的状态(明显的 q0∈ Q)。

F 是终止状态集合，也叫做接受状态的 Q 中的状态的集合(就是 F⊆Q)。2

接受器和识别器接受器和识别器（也叫做序列检测器）产生一个二元输出，说要么“是”要么“否”来回答输入是否被机器接受。所有FSM的状态被称为要么接受要么不接受。在所有输入都被处理了的时候，如果当前状态是接受状态，输入被接受，否则被拒绝。作为规则，输入是符号（字符）；动作不使用。

机器还可以被描述为定义了一个语言，它包含了这个机器所接受而非拒绝的所有字词；我们称这个语言被这个机器接受。通过定义，FSM接受的语言是正则语言 - 就是说，如果一个语言被某个FSM接受，那么它是正则的（cf. Kleene的定理）。

开始状态

开始状态通常用“没有起点的箭头”指向它来表示。

接受(终结)状态

接受状态（或称终结状态）是一个机器回报到目前为止，输入字符串属于它所接受的内容之状态。状态图中通常将其标示为双圆圈。

开始状态也可以是接受状态或终结状态，此情况下自动机会接受空字符串。如果开始状态不是接受状态，且没有可以连到任何接受状态的箭头，那么此自动机就不会“接受”任何输入。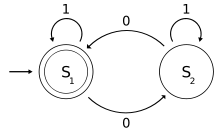

一个接受状态的例子如图：一台判断输入二进位字符串是否含有偶数个0的 确定有限自动机（DFA）。

S1代表着已经输入了偶数个0，因此S1 即为接受状态（同时亦为开始状态）。若输入含有偶数个0（包含没有0的字符串），则此机器会以接受状态来结束。

被这台DFA接受的字符串，举例来说是ε（空字符串）, 1, 11, 11…, 00, 010, 1010, 10110…等等。