[科普中国]-优化截取内嵌码块编码

JPEG2000 的基本结构如图1所示。首先对原始图像数据预处理，接着进行离散小波变换，然后在形成输出码流(比特流)之前，对变换系数进行量化、比特平面编码和算术解码，最后进行率失真控制和码流组织，形成压缩码流。压缩码流通过存储或传输后，进行与上述过程相反的变换后恢复出图像数据。1

EBCOT 算法是建立在码块(code-block)的基础上，将每个子带分成若干块，如 32x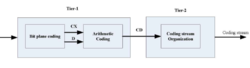32 或 64x64，每个码块独立编码，利用内部的相关特性进行压缩，对于每个码块再按质量进行分层，分成若干块段，各个块段之间就是截断点；选择一些码块和码块中的一些码段，就可以支持多分辨率和质量的码流结构。

EBCOT 算法可以分为 T1 和 T2 两部分，图2所示。T1包括比特平面编码、算术编码，负责数据的具体压缩；T2负责码流组织，主要根据压缩后率失真最优化算法(PCRD)实现的码流进行组织，并完成最后的打包工作。1

(1) 定质量解释：由于每个质量层可包含来自每个码块的任意贡献，质量的概念容易适应面向特定应用的显著性量度。与EZW和SPIHT和其他嵌入式压缩算法相比，当已知对应的空间区域或频带对某个应用并不重要时，EBCOT允许截断不需要的质量层数据。

(2) 灵活的结构：EBCOT 具有分辨率可伸缩性、失真可伸缩性(只要采用多重质量层)和一定程度的空间可伸缩性。当压缩多重图像分量(例如，彩色分量)时，这些分量构成了可伸缩性的第四维。JPEG2000 支持所有沿四维的渐进。

(3) 局部处理：独立编码允许对每个码块中的样本进行局部处理，这有利于硬件的实现。独立编码引入高度并行实现的可能性，其中多个码块可以同时进行编码和解码。

(4) 有效压缩：PCRD(压缩后率失真优化)算法可以更多的补偿由于施加独立块编码产生的效率损失，算法也能够适应空间变化和与图像有关的失真度量。

(5) 抗误码：在任何块编码的位流中遇到的误差对其他块编码没有影响，即所有JPEG2000 的码流都是分辨率可分割的。1

比特平面编码的任务就是生成数据的上下文信息，以供熵编码使用。它以码块为单位，扫描方式如图3所示。在某一比特平面上，一列中 4 个相邻的点组成一个条带。算法从第一个点(左上角)开始,依次扫描当前条带内的 4 个点，然后跳到右侧相邻条带，扫描到码块的右侧边界时，折回到左侧的下一条带。

码块的每个比特平面要经过 3 道扫描。重要性传播过程(SignificancePropagation Pass)，使用零编码 ZC 和符号编码 SC 原语编码；幅度细化过程(Magnitude Refinement Coding )，使用 MRC 原语编码；清理过程(Clear Pass )，使用游程编码 RLC 和符号编码 SC 原语编码。

很多情况下，子带的小波系数的高位比特平面出现全零的情况，编码从最高重要比特平面 MSB 开始可节约大量时间。每层比特平面按 3 道扫描顺序处理完该比特平面，然后再用同样的方法处理低一层的比特平面，直到第 0 比特平面处理完成，表明该码块的比特平面编码完成。1

具体的比特平面编码算法如下：

(1) 重要性传播， ：对于自己不重要但有重要邻居的系数进行ZC编码，如果系数由不重要变成重要则进行SC 编码。

(2) 幅值细化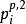， ：对于己经重要的且在当前比特平面没有编码的系数进行MR编码。

(3) 清理更新， ：对于自己不重要且未编码过的系数进行ZC或RLC 编码，如果有系数由不重要变成重要则进行SC 编码。这里又引入一个访问状态变量ηi[m,n]来表示 在当前比特平面是否编码过。

(4) ηi[m,n]置0，返回第1步进行下一个比特平面p-1的编码。2

算术编码是一种用于数据压缩的编码技术，它是基于 Shannon 定理的可变长的熵编码。算术编码的基本思想是用区域划分来表示信源输出序列，信源输出的任何一种组合，与[0 ,1) 区间内的某一区域一一对应。用算术方法表示这一区域为一个二进制小数。这个二进制小数是信源输出序列的一种编码，且它是唯一可解码的。算术编码的编码过程与信源的概率模型是分离的。在实际中使用概率估值表。1

T1编码器产生的比特流是内嵌的，利用率失真优化截取算法可以获得最优的压缩性能。设码块 在T1部分产生的内嵌比特流的码率截止到 ， 是某个截取点，即T1某个编码过程的结束点，则图像总的码率为：

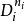设码块 的系数在恢复图像中产生的失真为 且其失真是加性的，即：

其中，D表示整幅图像的失真大小。

现在需要找到一组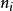 ，使得在满足 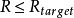时，D最小。解决这种条件极值问题可以通过拉格朗日算法。因此问题等价于使下式最小化：

其中调整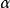 直到产生一组截取点使得上式在满足 时最小。对于上式最小化问题很可以归结为单个码块的最小化问题。即对于码块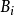 找到截取点 使得 最小。查找算法如下：

(1) 令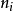 =0(即没有比特流)；

(2) 对于k=1,2,3…，计算 ， ；

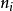(3) 若 ，则 =k。

由于这个算法要对不同的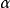 进行查找，因此先剔除一些奇异点，使率失真斜率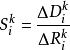随着k严格单调减。确定候选截取点算法如下：

(1) 令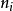 ={n}，n∈N，即所有过程的截止点；

(2) 令p=0；

(3) 对于 k，k∈ 。

计算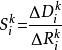，，。若p≠0且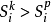，则从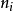剔除p并返回(2)；否则，令p=k。3