序言
现实世界中的许多问题都含有时变事件或时变参数 , 因此 , 关于时间的表示及其推理一直是哲学、物理学、计算机科学和人工智能领域的重要研究课题。然而,把时序推理引入AI还是近二十余年的事。而且,即使是现在,文献对时序问题仍未给予足够的重视。
某些工作也许更实际、更值得考虑,并使我们确信:时间的某种表示是必不可少的。例如,在医疗诊断中,显然需要表示 “事件(events) ” 和 “ 事件的过程(course-of-events) ”,即:不仅需要充分表达疾病的过程,而且需要指出疾病各个阶段的症状特征;为故事理解而开发的程序需要有过去时的表示法;而规划程序则需要一种表示可能的未来(possible future)的方法。1
早期的专家系统开发工具仅仅提供了一种基于规则的知识表示方法 , 这种方法简单且推理能力很有限 , 开发者在选择知识表示的元基、搜索策略、专用推理机时感到困难。新一代组合式专家系统开发工具 (Compsite Expert System Tool) 在功能、性能、用户接口、推理和效率等方面都比以往的专家系统开发工具有了很大提高 , 并且引入了时序推理机制。 2
一个需要时间表示及其推理的例子移动机器人的姿态 (attitude) 包括它在笛卡尔座标系中的位置参数x,y 以及方位角β。机器人在行驶时,β值是随时间而不断变化的。可以用性质TIME一VARYING来指明方位角β是机器人的一个时变属性。假定,带时标的 β取值情况如图1所示:使用时间点和时区等两种时标,其中,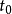 、
、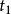 、…、
、…、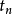 是绝对时间轴 t 上的时间点( time points );
是绝对时间轴 t 上的时间点( time points );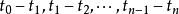 是时间轴 t 上的时区 (time intervals);在时间点5s处的β值为20°,在10一20s的时区 (time intervals) 内的β值为恒值30°,在时间点35s处的β值是10°。 在其余时间点和时区上的方位角β的 值未具体指定。可以设计并使用下列抽取方法 ( extraction method)来计算这些时间点和时区上的方位角β的值,乃至各种时序性质 (temporal properties) 和事件关系( event relationships ):
是时间轴 t 上的时区 (time intervals);在时间点5s处的β值为20°,在10一20s的时区 (time intervals) 内的β值为恒值30°,在时间点35s处的β值是10°。 在其余时间点和时区上的方位角β的 值未具体指定。可以设计并使用下列抽取方法 ( extraction method)来计算这些时间点和时区上的方位角β的值,乃至各种时序性质 (temporal properties) 和事件关系( event relationships ):
①EXACT——在未具体指定的时间 ( 时间点和时区 ) 上的月值为空;
②INTERPOLATE——如果时间处于两个时标之间,则用内插法求β值;否则,取最近的端点处的β值;
③VALID一UNTIL一CHANGED——取前一时标处的β值;
④VALID一FOR delta t——每个时标处的β值在时间轴t 的正方向外延delta t。
图2分别指出了在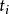 处如何求取β的值。
处如何求取β的值。 处为实测的β值。 1
处为实测的β值。 1
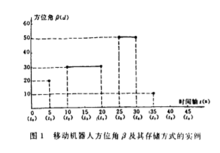

时序逻辑的一般概念若仅限于命题时序逻辑(propositional temporal logic)的话,那么,借助于命题演算连接词加上时序算子F,P,G和H,由某些原子句子就能产生出命题时序逻辑语言LT。换句话说,LT是命题演算语言的扩充,一个句子A可以成为FA,PA,GA和HA这样一些形式的句子,其中各算子的直观解释如下:
(1)FA——A在将来某时间为真;
(2)PA——A在过去某时间为真;
(3)GA——A在将永远为真;
(4)HA——A在过去一直为真。
要考虑真值随时间变化之一因素,基础模型论的结构必须包含“时间点”的概念以及时序优先关系。
定义 时序框架由时间点的非空集合T、时序优先关系R以及函数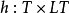 的原子句子
的原子句子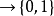 所构成。
所构成。
函数h在任意时间都把真值赋给每个原子句子,完整的LT的语义是通过把函数h按如下方法扩充到整个语言来传递的:
(1)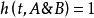 ,当且仅当
,当且仅当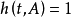 和
和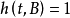 ;
;
(2)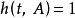 ,当且仅当
,当且仅当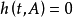 ;
;
(3)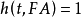 ,当且仅当
,当且仅当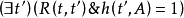 ;
;
(4)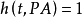 ,当且仅当
,当且仅当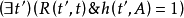 。
。
(3)和(4)反映了FA和PA的直观解释,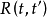 表示t的时序优先于t’。GA和HA的含义可以从下面的定义看出来:
表示t的时序优先于t’。GA和HA的含义可以从下面的定义看出来: ,
,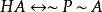
所以有:
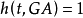 ,当且仅当
,当且仅当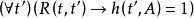 ;
;
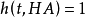 ,当且仅当
,当且仅当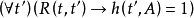 。
。
因此,可以说,如果一个句子在每个时间点上的取值都为1。则它在这种框架中为真。
通过改变R的性质就得到不同的逻辑。
不对关系R施加任何约束就得到最小时序逻辑K。其实,许多其他的时序逻辑系统都是最小时序逻辑的扩充,而且通过在时序优先关系上施以更多的约束而得到。例如,在R上施加如下两个约束就得到“分叉时间”( branching time)概念:
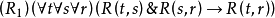
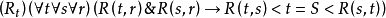 (两个小于号为∨)
(两个小于号为∨)
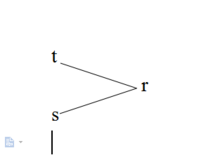
传递性(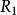 )隐含于所有时序优先概念之中:被称做反向线性(backwards Linearity)的条件(
)隐含于所有时序优先概念之中:被称做反向线性(backwards Linearity)的条件(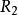 )消除了如图所示形式的时序继承中的分叉,因此分叉时间主张只有一个过去,但允许未来仍然是开放的。1
)消除了如图所示形式的时序继承中的分叉,因此分叉时间主张只有一个过去,但允许未来仍然是开放的。1
推理系统框架采用基于知识的提取方法,将所需知识分成4种类型:结构性知识、分类知识、时间语义知识和时间动态知识。根据不同的推理任务设计以下4种推理机构:上下文生成推理、同期推理、时间推理以及时间插值推理。推理系统的框架如图所示。 3
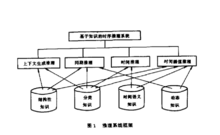
上下文生成推理只有在一定的上下文间隔范围内测得采样数据并进行知识提取才有意义。如:“第02号舰艇的导弹发射作为整个攻击任务中第一次突击的一部分攻击武器使用”。上下文间隔为解释创建一个相关的参考框架,使得系统只进行在指定上下文下有意义的知识提取,避免为无关上下文进行提取,上下文间隔的生成由上下文推理机制完成。上下文间隔的动态推理关系(DIRC)表示了上下文间隔和推出该上下文同隔的几种类型的命题(事件、参数、提取目标命题)的关系。
上下文间隔可以由提取目标间隔推出,可以由事件间隔推出,也可以由推出上下文间隔的参数命题(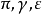 )的参数间隔推出,即参数π在上下文
)的参数间隔推出,即参数π在上下文 下的取值
下的取值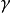 ,可以改变一个或多个参数的参考框架(如:导弹命中率在第一次突击时取值为低,会影响对毁伤程度值的解释)。
,可以改变一个或多个参数的参考框架(如:导弹命中率在第一次突击时取值为低,会影响对毁伤程度值的解释)。
生成上下文间隔的知识主要是结构性知识。如:事件命题,包括“是⋯⋯的一部分”;参数命题;解释上下文,包括“子上下文”关系;提取目标命题;一组上下文间隔的动态推理关系 (DIRC),基于“由⋯⋯推出”的关系。 3
同期推理同期推理以一个或多个参数点或参数间隔作为输入,输出为这些参数点或参数间隔的“状态”,即由采样数据归纳出某一状态值。所有时间参数的时向标记单位必须相同,如,某一任务以“天”作为最小时间单位,则在某一天内不同时间测得的参数具有相同的时间标记。 同期推理机制使用结构性知识(如:“⋯⋯提取为⋯⋯”关系),分类知识(某一参效按其值所在范围,可划分为高、中、低等),时间动态知识(指参数值在测量其值的时间点或时间间隔前 或后的一段时问内该值的可用情况。如,某一状态值的提取需考虑3个不同的参数,而这3个参数的值只能相距一段时间间隔依次测量,这就需要关于此3个参数的值保持情况的时间动态知识)。 同期推理用于两种相关任务:一种是分类任务,即对给定参数点或参数间隔内的参数值分类,如某一状态可有高、中、低3个值。需要的知识是状态值与对应参数取值范围的列表,这种分类与相关的解释上下文有关;另一种任务是分类任务的延伸,即计算转换,通过函数将已知 参数值映射为可进行提取的参数值,然后进行分类。 同期推理可进行单参数同期推理(一个参数对应一个状态)和多参数同期推理(多个参数对应一个状态)。 3
时间推理时间推理包括两种相关的推理:时间语义推理和时间同阶推理。
时间语义推理
时间语义推理使用参数命题的一组时间语义属性(如,向下继承,可连接等)进行推理。推理的输入可为一个提取参数间隔和一个时间(或上下文)间隔,输出为一个在时间(或上下文)同隔上的提取参数间隔;也可以为两个提取参数间隔,输出为一个由两个提取参数间隔新生成的时间间隔上解释的提取参数间隔。
在时间间隔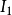 上成立的一些命题,可被推出在它的任何子间隔上成立,则这些命题就具有向下继承的时间语义属性,也就是说,这些命题的向下继承时间语义属性取值为真。
上成立的一些命题,可被推出在它的任何子间隔上成立,则这些命题就具有向下继承的时间语义属性,也就是说,这些命题的向下继承时间语义属性取值为真。
连接两个相邻的提取参数间隔生成一个长的时间间隔,需要另外一个时间语义属性,即可连接性。如果一个参数命题在任何两个相邻的连续时问间隔上成立,而且在这两个时间间隔相连而成的一个时间间隔上也成立,则该参数命题是可连接的。这种推理的输入为一个参数命题成立的两个提取参数问隔,输出为两个间隔连接而成的一个长间隔。
时间同阶推理
时间同阶推理确定同一上下文下两个相邻提取参数间隔进行连接操作(⊕)的值,其中同一参数的取值可能相同也可能不同(比如,一个为增加,一个为减少).推理除需使用时间语义知识外,还需使用同阶分类知识.同阶分类知识以同阶推理表的形式存储,同阶推理表由多个形如(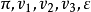 )的模式组成,其意义为在上下文
)的模式组成,其意义为在上下文 下参数
下参数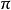 值为
值为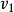 的提取问隔与值为
的提取问隔与值为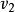 的提取同隔相连而成的连接提取问隔上的取值应为
的提取同隔相连而成的连接提取问隔上的取值应为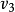 ,即
,即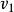 ⊕
⊕ =
=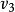 .3
.3
时间插值推理当两个需要连接的时间点和时间间隔不相邻时,则不能使用时间推理,而需使用时间插值推理。时间插值推理的输入为两个参数点或两个参数间隔或一个参数点和一个参数间隔,输出为通过在时间断开处插值形成的连接两个时间点(间隔)的时间同隔上的提取参数间隔。根据输入的不同,将插值分为两种类型的时间插值:1)一级插值:输入为两个参数点,输出为一个提取参数间隔;2)二级插值:输入为两个参数间隔(或一个参数点和一个参数间隔), 输出为一个大的提取参数间隔。又有3种最基本的提取类型(状态、趋势、速率),可组合为6种 插值任务。3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国