[科普中国]-线扩散函数

定义

线扩散函数(line spread function，LSF)的概念与点扩散函数的概念很相似。亮直线(通常是照明的狭缝)，通过光学系统成像后，亮度是往两侧散开的。其散开情况决定于成像系统的点扩散情况，这是因为这一亮点可以看做许多亮点组合所组成的，这许多点的扩散的堆积就构成了线像的亮度分布。

也就是说，线扩散函散是由点扩散函数堆积而成的。如果我们把像面上的线像长度方向叫做Y方向，那么线像沿x方向的亮度分布L(x)就叫做线扩散函数(一维表示法)。2

点扩散函数点扩散函数是点光源的像中光线的光照度或亮度的分布情况的数学描述。

点扩散函数的图象取决于衍射、散焦、像差和散射光线。在缺乏散焦、像差和散射的情况中，点扩散函数称为衍射极限点扩散函数，散焦、像差和散射光线使点扩散函数的图像变宽。

点扩散函数的图像还取决于孔径光阑的形状和直径。1

动态的线扩散函数当光电成像系统的成像特性在空间域和时间域内都满足线性和不变性条件时，则可以用动态线扩散函数来描述其动态成像特性。光电成像的动态线扩散函数取决予它的静态线扩散函数和脉冲响应函数，同时还与图像的运动速度有关。

右图为动态线扩散函数的图形。图中在空间坐标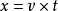处是静态的线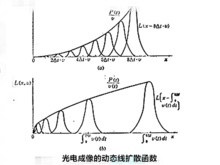扩散函数。由于运动使输入像移开，所以随着时间t的增加，该处的线扩散函数将按脉冲响应函数的规律衰减。同时由于运动使输入像移到新的坐标处，从而产生了连续的线扩散函数，由此构成了右图所示的动态线扩散函数的图形。

右图中的(a)图是匀速运动的动态线扩散函数，(b)图是变速运动的动态线扩散函数。

从右图中可以看出，动态的线扩散函数是沿位移坐标方向上一系列连续衰减的静态线扩散函数所叠加而成。用数学方法来描述，则动态线扩散函数等于静态线扩散函数与衰减曲线的卷积。这里所说的衰减曲线被定义为理想的动态线扩散函数。因为它是假定没有像差(即静态线扩散函数为狄拉克函数)时的动态线扩散函数。

现在建立理想的动态线扩散函数的表达式。首先令光电成像的静态线扩散函数为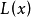，对于理想条件(即无象差系统)的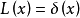同时令光电成像的时间脉冲响应函数为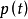。这时理想的动态线扩散函数可表示为。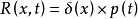

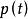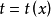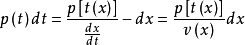上式右边的卷积所取的变量不一致，应将函数的时间变量转换为空间坐标变量。取，由于，所以。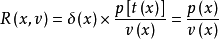

式中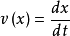是输出像面的运动速度，这是所确定的理想状态的线扩散函数是坐标x和像速v的图像。

根据据上述分析，并考虑到光电成像的静态像差与动态滞后两者是不相关的，因此可以通过静态线扩散函数与理想动态线扩散函数的卷积来确定光电成像的实际线扩散函数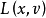，即：

上式即光电成像动态线扩散函数的通用表达式。3