[科普中国]-气动辅助变轨

研究的背景和意义

未来的载人空间站系统是以空间站为核心，由同轨平台、极轨平台、自由飞行卫星及空间交通工具——轨道机动飞行器组成。轨道机动或转移航天器往 返于空间站与平台、卫星等飞行器之间，他们的变轨可用冲量或连续推力方 式，但是耗能比较大，而气动力辅助轨道转移可成为节省燃料的变轨方案。气 动力辅助轨道转移概念的提出始于六十年代，1961年H.London在美国宇航学 会上正式提交了一份论文，论证了气动力辅助轨道转移的意义与可行性。自此 揭开了气动力辅助轨道转移研究的序幕，四十多年来，世界各航天器气动力辅助变轨方法研究国的许多专家学者都参与了这一具有重大发展前景的课题的研究，尤其是自九十年代以后，关 于气动力辅助轨道转移的研究掀起了一个热潮，从各个方面对气动力辅助轨道 转移问题进行了研究。

AOT(Aeroassisted Orbit Transfer)的概念最早由London提出的，并由其论 证了实现的可行性。所谓气动力辅助轨道转移，是把纯冲量变轨与气动力变轨结合起来，在整个变轨飞行中插入大气飞行段。在该段飞行中借助气动力 完成部分变轨(改变轨道平面或高度)，最终以最小耗能等技术指标完成全部变 轨要求。

气动力辅助变轨与冲量变轨或者连续推力变轨比较，主要差别是：在完成 高能量到低能量轨道转移时，前者能量消耗主要靠气动力，后者主要靠燃料的 喷射；在完成轨道平面变换时，前者以气动力为辅助手段完成部分轨道倾角变 化，后者主要靠燃料的反作用改变倾角；在设计转移轨道时，前者需要有意插 入一段大气层内轨道转移，后者则无此要求。气动力辅助变轨主要适用于低地 轨道和同步地球轨道或者其他深空高轨道之间的往返联系以及大轨道平面倾角 变化的异面轨道变轨。

AOT变轨方式由于有效的利用了航天器环绕星球上的大气这种自然资源，借助气动力减少了燃料消耗，从而使飞行器获得了较大的有效载荷比。由 于这种变轨方式可以大大节省变轨所需的燃料，因此普遍认为AOT是未来空 间运输的很重要的手段之一。我国将要发展先进的空间运输系统，利用以上技 术会带来巨大的经济效益。因此这也就是研究气动力辅助轨道转移这个课题的原因。1

气动力辅助变轨发展气动力辅助变轨1961年Howard London在美国宇航学会第二十九届年会上正式提交了一 份论文，论证了应用AOT的意义和可行性。四十多年来，美、欧等国家的许 多专家、学者都在从事着方面的研究，在我国这项技术还处于起步阶段，在近 些年来，哈尔滨工业大学、北京航空航天大学和西北工业大学等单位的部分专家学者已开始重视这项技术研究，并取得了一定的研究成果。

在对气动力辅助轨道转移的研究主要集中在两个方面，第一阶段主要针对气动力辅助轨道转移的最优轨迹的研究，第二阶段是气动力复转轨道转移的最 优控制律的研究。由于在AOT变轨过程中插入了大气段飞行，故必须制定适 当的控制律控制，使OTV在大气内完成相应的变轨要求，并最终能逸出大气 到达目标轨道。

气动力辅助变轨的应用主要有三个方面：

气动力辅助轨道变换轨道平面变换是气动力辅助轨道研究的最初研究目的，也是最早提出的， 典型的最优脱离轨道变轨如下：

首先，由特征点a加一反向冲量ΔV1，使航天器脱离HEO(High Earth Orbit) 进入转移轨道，转移轨道内切HEO于特点a，在大气边界特点b进入大气 层，利用升力控制卫星在大气层内的飞行，使之在c点冲出大气层，同时在c 点施加第二个速度冲量ΔV2(如果速度足够，c点可以不加冲量)，使航天器运行 至d点并于LEO(Low Earth Orbit)内切，同时加速度冲量ΔV，完成过渡全过 程，如图1-1。

家学者已开始重视这项技术研究，并取得了一定的研究成果。

在对气动力辅助轨道转移的研究主要集中在两个方面，第一阶段主要针对

气动力辅助轨道转移的最优轨迹的研究，第二阶段是气动力复转轨道转移的最优控制律的研究。由于在AOT变轨过程中插入了大气段飞行，故必须制定适 当的控制律控制，使OTV在大气内完成相应的变轨要求，并最终能逸出大气 到达目标轨道。

最优大气辅助变轨研究的进展一个航天器在某个星球的大气中飞行，将受到两种自然力：气动力和引力 的作用，气动力是因飞行体与大气的相对运动而诱发产生的，包括了星球的旋 转和其他因素引起的大气扰动。气动力还是飞行体的气动外形、飞行速度和高 度的函数，因而与逆平方率的引力不同。这种自然力的作用被人类认识研究并 加以利用，对人类文明和科学的演进产生了巨大影响。19世纪初数学、力学和 技术科学的蓬勃发展，促进了宇航科学的发展，人们对气动力的作用有了系统 的理论认识，把它作为一个辅助利用来优化飞行体的轨道和最佳控制其飞行， 可获得惊人的能量节省。

气动力辅助变轨始于London所写的有关卫星变轨的论文，自此以后，人 们对这个问题的研究取得了很大进展。Vinh在20世纪70年代就开始研究大气 层中航天器的运动特性和优化轨道理论。Walberg于1985年对气动力辅助变轨 作了系统全面的总结与评述142篇文献，Mease就气动力辅助变轨的优化问 题作了评述，Miele近期就气动力辅助变轨的优化与制导新进展作了较系统的 介绍，主要反映他和他的合作者的研究工作，综述了99篇文献。AOTV的 最优大气辅助变轨，在大气飞行段包括再入、大气飞行及逸出大气层等几个阶 段，过程比较复杂，而且在宇航工程应用中在产生经济效益方面发挥出越来越 大的作用，故引起国内外许多科学家的广泛重视，并开展了大量的研究工作。 Miele提出了大气辅助变轨研究中的9种主要性能指标

1、动力变轨的燃料消耗量最小；

2、大气飞行段的总加热量最小；

3、大气飞行段的飞行时间最小；

4、大气飞行段的飞行时间最大；

5、大气飞行段弹道倾角平方的积分最小；

6、进入与逸出大气层的弹道倾角的平方和最小；

7、大气飞行段的峰值热流最小；

8、大气飞行段的峰值动压最小；

9、大气飞行段的最低飞行高度最大。

前6类性能指标为化为终端型性能指标，后3种性能指标为Chebyshev型 性能指标。Miele和他的同事利用序列梯度恢复法对同面轨道、异面轨道的大 气辅助过程进行了大量的计算。结果表明，对于平面大气辅助变轨，性能指 标1和5的最优结果是类似的，对于异面变轨，利用性能指标5得到的结果虽然动力变轨的速度增量与性能指标1相比略有增加，但峰值动压和峰值热流大 幅度下降，因此，它提供的结果更为优越。

Vinh和Hull及其他作者，国内哈工大的杨涤、吴瑶华，西工大的陈 士橹、吕学富等对大气辅助平面变轨、异面变轨进行了研究，得到了大量 的结果。

Vinh和Lu P.推导了采用极大值原理处理Chebyshev问题的方法，将问题 化为沿轨道状态变量受约束的问题来研究气动滑行。Vinh和Mease研究了大 气巡航的最优特性，指出这种辅助变轨方式对于大幅度改变近地轨道的倾角是 优越的。Vinh和Ma D.M.对多次通过大气层的变轨过程进行了分析，因为一 次通过大气层时，航天器要承受很大的气动加热，而多次通过大气层是一个较 好的解决办法，但是，对于载人飞行，考虑到范阿伦辐射带的影响，多次通过 大气层时不适合的。

沿飞行轨迹最大加热热流，最大过载受到限制，这是基于结构质量和宇航 员的生理条件约束问题，Hiele.Chern和Vinh.Lee和Hull对这一问题进行了研 究，国内这方面研究比较少。

在未来的空间交会对接和反卫星武器系统中，气动力辅助拦截和交会将会 起到非常重要的作用。它和一般的变轨不同之处主要在于终端条件，其优化目 标也不仅仅局限于燃料消耗最少，有时需要其拦截时间最小或轨道的倾角改变 量最大，以及脱靶量最小等，作为一般军事目的的拦截和空间交会国内外研究 较多，但是这些研究都不是基于气动力辅助变轨技术。Horie和Conway研究 推力为零情况下的气动力辅助拦截问题，并就时间最小和耗能最小给出数值算 例。但是从军事目的出发，优化目标函数往往是复合的，如时间最小和脱靶 最小，以及能耗最小和时间最小。另外推力协同气动力辅助变轨，对增加拦截 和交会AOTV的机动性能和缩短飞行时间将具有现实工程应用意义。

推力协同在气动力辅助变轨中的作用，尽管在20世纪60年代就有人研究 过，但是近年来又引起许多科学家的关注，并得到了许多新结论。Ross和 他的合作者以及Park，Caoalino等对气动力辅助机动，协同机动，气动力砰 击，气动力巡航机动等的研究，极大地推动了气动力辅助变轨与控制的进展。 气动力辅助变轨技术，已在星际航行得到了广泛应用。值得进一步讨论的是星际航行中利用星球的大气层，实现辅助引力转弯问题。气动力辅助引力转 弯时20年前美国捧起推进实验室提出的一种气动力辅助变轨概念，用于星际 航行变轨。当带有升力体的飞行器飞过某星球的大气层时，其升力矢量相对 星球体中心时，将比纯引力转弯获得更大的速度增量，因而可降低发射能量和 缩短飞行时间。随着星际探测任务被提到日程，对气动力辅助引力转弯的研究 越来越深入。

基于气动力辅助变轨的变气动外形飞行器的讨论是作者今年的研究课题之 一。早在20世纪80年代Andrews，Grenich等人实验性地研究充气囊变 阻轨道器作为气动制动的AOTV应用于空间运输系统。这个新概念，近期被俄罗斯宇航界应用到再入飞行器和弹头回收。航天器的气动外形对在大气层 内飞行中的热流、过载和机动性，以及最优成本都有决定性的作用。但是要满 足全面的性能要求，很难找到一个理想的气动外形，特别是一个固定的气动外 形飞行器，因而，出现各种类型的带有气动制动器或捕获装置，或可变气囊， 或可展的阻力裙，在给定的飞行阶段，来改变飞行器的升阻比L/D和弹道系 数，以适应不同飞行任务要求。

稀薄气体动力学发展现状研究超低轨道航天器，就必须研究高层大气产生的气动力与气动力矩对卫 星姿态和轨道的影响，由于超低轨道卫星飞行高度的环境中，大气密度极低， 平均分子自由程与卫星特征长度相比十分接近，因此气动力方面的研究主要是 稀薄气体动力学的研究。

国外在这方面早有理论上的研究，19世纪麦克斯韦利用平均自由程的概念 求得了气体输运系数，玻尔兹曼建立了分子运动速度分布函数的积分-微分方 程，即玻尔兹曼方程。1946年，钱学森最先利用努森数Kn，根据气体的稀薄 程度将稀薄气体流动分为四大领域：连续流领域、滑流领域、过渡领域、自由 分子流领域，并且提出了许多稀薄气体动力学发展的关键性问题。至今，对于 解决稀薄气体动力学问题的基本方法为解玻尔兹曼方程，具体实现有两大类： 分析方法和数值方法。分析方法主要有矩方程或输运方程方法、模型方程方 法、运动论边值问题的变分方法等；而数值方法主要就是蒙特卡洛方法，又 被分为直接模拟蒙特卡洛方法(DSMC)、试验单元蒙特卡洛方法(TPMC)等，这 类方法不解玻尔兹曼方程，而在计算机上用统计取样模拟气体分子的运动和碰 撞过程，其中澳大利亚的Bird提出的直接模拟蒙特卡洛方法在航天飞机上得 到了实际的验证；此外还有对碰撞积分进行数字积分，直接解玻尔兹曼方程 的方法，如间断纵坐标方法等。

国内在这方面起步较晚，但是成果也有很多，主要有中科院的沈青在研究 改进直接模拟蒙特卡洛方法的计算机算法，提出了表面元算法来提高直接模拟 蒙塔特卡罗算法的效率，并且作为863计划的一个项目研制了通用软件；此 外，国防科技大学的吴其芬也在这方面编写了一本稀薄气体动力学专著[28]。 早期，航天器气动力与气动力矩的计算基本采用近似的方法，假定某一气动阻力系数，带入解析式计算出气动力后，假设质心与压心之间的矢径是包括 全部附件在内的航天器最大尺寸的三分之一，进而通过力乘力臂的方式得到 卫星受到的气动力矩，但是这仅仅是保守的估计值。当前，出现了计算机后， 对气动力与气动力矩的计算就有了很大的发展。对于气动力计算的软件编制方 面，国外已经有比较完善的理论计算公式和计算方法来进行建模和程序编制， 其中就包括经验公式和直接模拟蒙特卡洛方法。早期的卫星设计者们使用的主 要是经验公式。当前，国外已经发展了许多计算软件：直接模拟蒙特卡洛方法 的创立者Bird开发了DS2V/DS3V程序，能够对二维或三维任意外形物体的气 动力与气动力矩进行直接模拟蒙特卡洛方法的计算，程序说明也比较详细，主 要问题就是软件中导入三维模型的前期处理繁琐并需要其他特殊的软件，计算 气动力与气动力矩的时间比较长，占用大量CPU和内存，并没有提示说明计哈尔滨工业大学工学硕士学位论文算结果已经收敛稳定；英国Cranfield大学的空间研究中心研发了环数据分析工具(Spacecraft Engineering,Design,and Analysis Tools:SEDAT)软件，利用的是自由分子流的公式并结合气体与物体表面反应的模型、光线追踪方法和试验单元蒙特卡洛方法进行的编程，而且已经为欧空局的空间碎片收集卫星计划进行了计算，但是庞大而复杂的数据对计算过程产生了巨大的影响。另外，俄罗斯也根据直接模拟蒙特卡洛方法研制了计算气动力的软件 SMILE(Statistical Modeling In Low-Density Environment)，Ivanov等人计算了进 步号飞船的气动力。

在国内，这方面的气动力计算主要应用于载人航天器返回的精确制导，预 估返回舱进入大气层飞行期间的各向载荷分布，评估气动稳定性，确定飞行轨道。载人飞船返回经历的自由分子流和过度流区，主要采用蒙特卡洛方法和近 似计算方法来得到气动力量值。

有限推力变轨及其研究进展自从R.H.Goddard对在两点间的航天器最优转移轨道问题提出在能量消耗 最少情况下的最优近似解法以来，这一问题引起了学术界的广泛关注。1959 年，Hohman解决了在共面圆轨道间转移的最小特征速度这一基本问题。此 后，Marec从理论上做出了精确的证明，Marchal把Hohmann理论应用于椭圆轨道间的转移，Smith研究了椭圆和圆轨道之间的转移，McCue则研究了 非共面轨道之间的转移，Eckela和vinh研究了固定时间和固定燃料下的 Hohmann轨道转移问题。

Hoelker和Silber第一次提出三次变轨问题并验证了这种变轨要优于 Hohmann转移。Roth借此研究了非共面椭圆轨道间转移。之后，Prussing、 Glickman和Bercaw进行了多次冲量下的最优轨道转移问题的研究。Redding 和Matogawa继续将这一思想加以推广，得出了轨道以有限推力进行多次变轨 能够达到最优的结果。

还有一些学者进行脉冲式变轨研究是通过转移次数作为变量而不是固定的 值，从事这方面的工作者主要有Handelsman，Jezewski和Rosendaal，Gross和 Prussing，Eckel、Prussing和Chiu。该方法的出发点是Lawden开创的矢量 力学。Antoi Fernando BertaChinide Almeida Prod通过数值方法进行有限推力下哈尔滨工业大学工学硕士学位论文的轨道转移问题研究，该方法先用于推力方向固定的情况下，然后对推力方向 进行多次取初值来计算能量损失，通过比较不同的结果找到最优方案。可见， 该方法的计算量是较大的，而且假定变轨过程中推力方向不变是有局限性的。 但是在实际的工作过程中，没有必要假定推力方向不变，发动机推力方向是时 时变化的，这样对节省能量也是有好处的。

轨道优化理论与最优控制的研究进展在有限推力变轨、大气辅助变轨的最优化研究中，我们所要寻找的是一条 最优飞行轨迹，这是过程优化或最优控制问题，从工程应用角度称为轨迹优 化，这类问题很早就得到了科技界的重视。从20世纪30年代开始，Caratheodory在古典变分法基础上开始研究最优化方法，但是直到计算机的出 现，最优化方法才真正用于工程实践中。例如20世纪50年代，钱学森用古 典变分法研究了探空火箭在大气中的垂直上升的最大飞行高度问题，获得了满 意的结果，并在以后的探空火箭设计中得到了应用，这项工作对以后的轨迹优 化研究产生了重要的影响。

古典变分法所能解决的问题是有限的，它无法处理某些变量受到约束或发 生突变的情况，即使对于探空火箭垂直上升这样一个简单问题，也必须作大量 的假设，而所得结果还包含起飞冲量这样一个实际设计中难以实现的过程。20 世纪50年代，俄罗斯学者Pontryagin等人在古典变分法的基础上，将变量 区分为状态变量和控制变量，讨论了有界控制下纯状态约束的优化问题，给出 了庞特里压金极大值原理的共同点就是通过最优性能分析，控制函数能够表示 成状态变量和附加的伴随变量函数，然后化为两点边值问题求解，由于不是对 性能指标函数直接寻优，因此称为间接法。常用数值方法求解，一种最广泛的 方法是打靶法和多次打靶法。庞特里压金的合作者之一格姆克列里兹在他的研 究中，对最优控制理论中的变分法作了完整的、严格的证明。Hartl等人就具有状态约束的最优控制问题的极大值原理和其应用作了全面的介绍。1

国内有许多学者在这个领域作了很深研究。杰出科学家钱学森在二次世界 大战结束前后对弹道火箭及其控制的研究中，特别是解决优化方法与反馈控制 技术和理论问题，发展成一门新的学科——工程控制论，并在1945年出版了 《Engineering Cybernetics》，为世人所瞩目，是该领域最早的开拓者 。哈尔滨工业大学工学硕士学位论文值得指出，控制论学者Berkovitz于1961年就提出变分方法，1974年对优 化控制过程给出严格的数学理论。Bell和Jacobson在1975年就系统的研究奇 异优化控制理论。随着推力协同引入气动力辅助变轨，奇异优化控制问题今年 来受到学术界极大的关注，并取得突破性进展，集中表现在对极值弧，特别是 奇异弧，开关结构的特性，连接条件和相关的控制律研究，这些研究有力的推 动了飞行器的优化设计，并对过去长期研究结论提出质疑。

直接解法较间接法大约早了一个世纪，可追溯到1874年Cauchy的梯度法。20世纪50年代，贝尔曼，Bryson，Denham，Mikamn等人研究了求解最 优过程问题的数值方法，如贝尔曼动态规划法、一阶梯度法、二阶梯度法等， 尤其值得注意的是贝尔曼动态规划法，它的解是全局最优解。Miele等人从60 年代开始研究序列梯度恢复法，近十年来用该方法对最优大气辅助变轨过程进 行了研究，证明是一种较好的方法。Betts，Enright等人讨论了稀疏非线性规划法、非线性规划法以及直接有限元转移法等，Hargraves和Herman等人讨 论了直接配点非线性规划法，以及最近Fahroo和Ross的Legendre伪谱线法是十分有效简便方法。这些方法将方程沿飞行轨迹离散化，微分方程作为离散变量之间的约束，直接采用参数优化的方法进行求解。这些方法的共同特点是对指标函数直接寻优，因此成为直接法。直接法的最近进展是应用微分几何的微分包含来表示一个动力学系统的状态变量导数所构成的一个集，并将状态速率约束在一个可行的空间。由此优化解仅仅是状态变量在节点上的离散，而不必考虑控制变量，故既是低维的，又适用奇异控制问题的求解，且增加了鲁棒性。2

气动辅助变轨阶段气动辅助变轨方法

并假设切向速度增量 等于法向速度增量除以最大升阻比(取 1.8)，且为负值。 高度的圆轨道所需速度气动辅助变轨可分为3个阶段:共面离轨段、气动辅助异面变轨段和共面升轨段。增量 Hohmann变轨公式可求。

HEO-LEO 共面变轨，初始 HEO 轨道为赤道圆轨道，轨道半径为 r1;目标 LEO 轨道亦为赤道圆轨道， 轨道半径为 r2。

a)共面离轨段:首先施加一个离轨速度增量 椭圆转移轨道，椭圆转移轨道的近地点在大气层内，两者处于同一轨道面内。

b)气动辅助异面变轨段:进入大气层后，进行气 动辅助异面变轨机动，获得法向速度增量，完成轨道 平面的改变。

a)共面升轨段:气动辅助异面变轨完成后，飞行 器到达大气层的边缘并施加一次脉冲轨道机动加速轨 因此，得到 LEO-LEO 异面变轨节省燃料条件为: 在对应的圆轨道高度上，轨道倾角 改变大于临界变轨角度时，气动辅助变轨才节省燃料。 道机动 椭圆轨道。当到达椭圆轨道的远地点时，再施加一次速度增量 如果想通过气动辅助变轨节省燃料，其任务剖面必须满足一定的条件:

1)对于 HEO-LEO 共面变轨，对应不同的目标圆 轨道高度，当初始圆轨道高度大于表 中对应的临界初始圆轨道高度时，气动辅助变轨才节省燃料。

2)对于 LEO-LEO 异面变轨，对应不同的圆轨道 高度，当轨道倾角 改变大于表 中对应的临界变轨角度时，气动辅助变轨才节省燃料。3

气动辅助转移的方程假设行星的大气是不旋转的,并且大气的密度随高度以指数变化。探测器在大气中的运动方程如下:

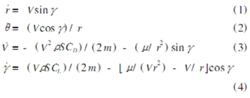
阻力系数取抛物线型阻力极线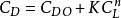 ,假设升阻比L/D为常值,则可以推导出AGA转移中,探测器飞出时的双曲线超速V∞2与飞行器在大气中飞过转角θ的关系:

这里μ和r分别是借力天体的引力常数和探测器距离借力天体中心的半径。探测器在大气中飞过的转角θ可由下式得到:

AGA转移总的转角