[科普中国]-方向数

方向数就是既有方向又有数值的一种向量表达方式，比如{1，1，1}就是边长为1的正方体的立体对角线，计算其长度就是把三个边长平方相加再开方。直线的任一方向向量的坐标m、n、p叫做这直线的一组方向数。

简单介绍如果一个非零向量平行于一条已知直线，这个向量就叫做这条直线的方向向量。

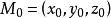由于过空间一点可作而且只能作一条直线平行于一已知直线，所以当直线L上一点 和它的一方向向量 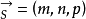为已知时，直线L的位置就完全确定了。

直线的任一方向向量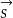 的坐标m、n、p叫做这直线的一组方向数1。

当方向数没能对应在正方体或者长方体上面，而是在三维坐标图中时，可以自己想象一个长方体出来，其长、宽、高就是{长，宽，高}，这个表达形式就是方向数。把长宽高的平方和开方，得到的就是这个方向数的长度，既长方体的立体对角线。

方向数与方向余弦方向数、方向余弦可以用来确定空间有向直线的方向，但是如果只需要确定一条空间直线的方位（一条直线的两个方向均确定着同一方位），那末就不一定需要知道方向余弦，而只要知道与方向余弦成比例的三个数就可以了。这三个与方向余弦成比例且不全为零的数A，B，C称为空间直线的方向数，记作：{A，B，C}，即：

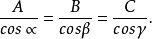据此可得到方向余弦与方向数的转换公式：

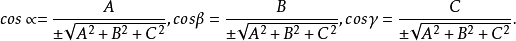
其中，根式取正负号分别得到两组方向余弦，它们代表两个相反的方向。

关于方向数的问题空间任意两点坐标之差就是联结此两点直线的一组方向数。

方向数求夹角设L1与L2是空间的任意两条直线，它们可能相交，也可能不相交。通过原点O作平行与两条直线的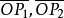线段 ，则线段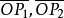 的夹角称为此两直线L1与L2的夹角。

若知道L1与L2的方向数，则有公式为：

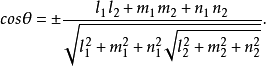
方向数判别两直线平行、垂直两直线平行的充分必要条件为：

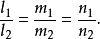两直线平行的充分必要条件为：

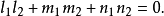
方向数和方向向量的关系方向数是方向向量在相应坐标轴上的投影，或者说方向数是方向向量的数字描述。方向数是指坐标向量的数据，如：向量a=（1，2），而方向向量也可能是非坐标向量下的向量。方向数一定是方向向量，但方向向量不一定是方向数。

例如：过点M（1，3，5）且方向数为{2，1，2}的直线方程为（x-1）/2=（y-3）/1=（x-5）/2；这条直线与向量a=2i+j+2k平行。另外，也可作图验证：画个立体直角坐标,画出点A（2，1，2），连接OA，这就是所求直线的方向向量a；再画出点M（1，3，5）；再任取m=1，算出x=2m+1=3，y=m+3=4，z=2m+5=7，画出
点N（3，4，7），再连接MN。最后观察出MN与OA平行。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学