[科普中国]-再生核

再生核又称为重建核，它定量地给出了小波基的相关性和冗余性。如果变换系数之间有一定的相关性（不正交），就可能从其中一个变换系数恢复（或再生）出另外一个变换系数，因此，再生核的称谓由此得来。

简介再生核又称为重建核，它定量地给出了小波基的相关性和冗余性。

从小波基函数的定义可以猜想，如果a，τ参数连续变化，得到的小波基将是冗余的。或者这样理解：如果在尺度-位移平面上的两个点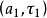 和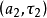 很靠近，那么得到的小波基函数 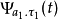和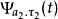 形状和大小很接近，位置也很靠近，它们具有很强的相关性，而且随着两个点的更加靠近，相关性增强，反之则相关性减弱。存在相关性就意味着不正交（因为根据概率论的知识，正交必定不相关），因此就存在着冗余。

推论尺度-位移连续变化的小波基函数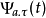 形成了一组非正交的过度完全基。其中的“过度”表示这一组基含有冗余性，“完全”表示这一组基可以完全覆盖整个尺度一位移平面，这样，任意一个信号都可以用这些基来分解表示。在 a-τ平面上任意两点 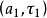和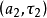 ，其对应的小波基函数之间究竟有多大的相关性，这就需要用再生核来描述和刻画。从再生核的定义式，即

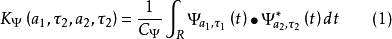
可以看出，式(1)实质上是计算函数内积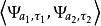 ，只是比例系数稍有不同。在数学上，内积实质上表示了两个函数的“相似”程度。如果两个信号矢量 与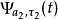 完全垂直，那么内积 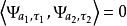再生核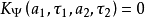 表示两个信号矢量完全不相关。如果矢量 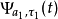与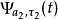 完全平行，那么内积 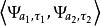和再生核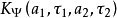 都分别取得最大值，表示两个信号矢量完全相关。式(1)中的系数为

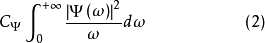
表征了a-τ平面上任意两点对应的小波基函数之间的相关性，此外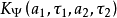， 也可以表征连续小波变换系数 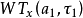和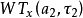 之间的相关性大小。如果变换系数之间有一定的相关性（不正交），就可能从其中一个变换系数恢复（或再生）出另外一个变换系数，因此，再生核的称谓由此得来。实际上，要完全准确恢复出 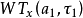，仅仅依靠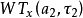 是不够的，通过 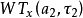只能提供部分恢复信息，如果将 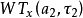的“部分贡献”表示为

再生核方程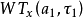 的完全准确恢复需要a-τ平面上无数个类似于 的点的共同贡献才能完成，这种无限多个贡献的累积就归结为a-τ平面上的二维积分，即

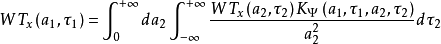
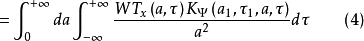
式(4)称为重建核方程（或再生核方程）。1

本词条内容贡献者为:

胡建平 - 副教授 - 西北工业大学