简介
非负矩阵分解由Lee和Seung于1999年在自然杂志上提出,它使分解后的所有分量均为非负值(要求纯加性的描述),并且同时实现非线性的维数约减。NMF的心理学和生理学构造依据是对整体的感知由对组成整体的部分的感知构成的(纯加性的),这也符合直观的理解:整体是由部分组成的,因此它在某种意义上抓住了智能数据描述的本质.此外,这种非负性的限制导致了相应描述在一定程度上的稀疏性,稀疏性的表述已被证明是介于完全分布式的描述和单一活跃分量的描述之间的一种有效数据描述形式。
因为纯加性的和稀疏的描述能使对数据的解释变得方便(少量活跃的分量使数据的组成方式变得清晰)与合理(许多物理信号中不可能存在负饷成分),还因为相对稀疏性的表示方式能在一定程度上抑制由外界变化(如:部分遮挡、光照变化和物体的旋转等)给特征提取带来的不利影响,所以NMF已逐渐成为信号处理、生物医学工程、模式识别、计算机视觉和图像工程等研究领域中最受欢迎的多维数据处理工具之一。具体说,它日前已被应用到文本分析与聚类、数字水印、人脸检测与识别、图像检索、图像复原、语言建模、声源分类、音乐信号分析与乐器识别、盲信号分离、网络安全、基因及细胞分析等的研究中。
定义对一个M维的随机向量 ,进行了
,进行了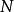 次的观测,记这些观测为
次的观测,记这些观测为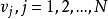 ,取
,取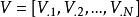 ,其中
,其中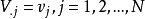 ,NMF的目标是求出非负的M×L的基矩阵
,NMF的目标是求出非负的M×L的基矩阵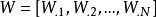 和
和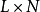 的系数矩阵
的系数矩阵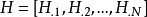 ,使得
,使得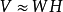 ,用矩阵表示为
,用矩阵表示为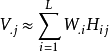 。
。
从多元统计的观点看,NMF是在非负性的限制下,在尽可能保持信息不变的情况下,将高维的随机模式简化为低维的随机模式H,而这种简化的基础是估计出数据中的本质结构W;从代数的观点看,NMF是发现数据的一种内在非负(或蕴涵更多性质的)代数分解形式或表示方法;从维数约减的观点看,因为基矩阵W和系数矩阵H同时由NMF来确定,系数矩阵H并非为数据矩阵V在W上的投影,所以NMF实现的是非线性的维数约减2。
应用NMF的广泛应用,源于其对事物的局部特性有很好的解释。在众多应用中,NMF能被用于发现数据库中的图像特征,便于快速自动识别应用;能够发现文档的语义相关度,用于信息自动索引和提取;能够在DNA阵列分析中识别基因等等。我们将对此作一些大致的描述。
图像分析NMF最成功的一类应用是在图像的分析和处理领域。图像本身包含大量的数据,计算机一般将图像的信息按照矩阵的形式进行存放,针对图像的识别、分析和处理也是在矩阵的基础上进行的。这些特点使得NMF方法能很好地与图像分析处理相结合。人们已经利用NMF算法,对卫星发回的图像进行处理,以自动辨别太空中的垃圾碎片;使用NMF算法对天文望远镜拍摄到的图像进行分析,有助于天文学家识别星体;美国还尝试在机场安装由NMF算法驱动的识别系统,根据事先输入计算机的恐怖分子的特征图像库来自动识别进出机场的可疑恐怖分子。
文本聚类/数据挖掘文本在人类日常接触的信息中占有很大分量,为了更快更精确地从大量的文本数据中取得所需要的信息,针对文本信息处理的研究一直没有停止过。文本数据不光信息量大,而且一般是无结构的。此外,典型的文本数据通常以矩阵的形式被计算机处理,此时的数据矩阵具有高维稀疏的特征,因此,对大规模文本信息进行处理分析的另一个障碍便是如何削减原始数据的维数。NMF算法正是解决这方面难题的一种新手段。NMF在挖掘用户所需数据和进行文本聚类研究中都有着成功的应用例子。由于NMF算法在处理文本数据方面的高效性,著名的商业数据库软件Oracle在其第10版中专门利用NMF算法来进行文本特征的提取和分类。为什么NMF对于文本信息提取得很好呢?原因在于智能文本处理的核心问题是以一种能捕获语义或相关信息的方式来表示文本,但是传统的常用分析方法仅仅是对词进行统计,而不考虑其他的信息。而NMF不同,它往往能达到表示信息的局部之间相关关系的效果,从而获得更好的处理结果。
语音处理语音的自动识别一直是计算机科学家努力的方向,也是未来智能应用实现的基础技术。语音同样包含大量的数据信息,识别语音的过程也是对这些信息处理的过程。NMF算法在这方面也为我们提供了一种新方法,在已有的应用中,NMF算法成功实现了有效的语音特征提取,并且由于NMF算法的快速性,对实现机器的实时语音识别有着促进意义。也有使用NMF方法进行音乐分析的应用。复调音乐的识别是个很困难的问题,三菱研究所和MIT(麻省理工学院)的科学家合作,利用NMF从演奏中的复调音乐中识别出各个调子,并将它们分别记录下来。实验结果表明,这种采用NMF算法的方法不光简单,而且无须基于知识库。
机器人控制如何快速准确地让机器人识别周围的物体对于机器人研究具有重要的意义,因为这是机器人能迅速作出相应反应和动作的基础。机器人通过传感器获得周围环境的图像信息,这些图像信息也是以矩阵的形式存储的。已经有研究人员采用NMF算法实现了机器人对周围对象的快速识别,根据现有的研究资料显示,识别的准确率达到了80%以上。
生物医学工程和化学工程生物医学和化学研究中,也常常需要借助计算机来分析处理试验的数据,往往一些烦杂的数据会耗费研究人员的过多精力。NMF算法也为这些数据的处理提供了一种新的高效快速的途径。科学家将NMF方法用于处理核医学中的电子发射过程的动态连续图像,有效地从这些动态图像中提取所需要的特征。NMF还可以应用到遗传学和药物发现中。因为NMF的分解不出现负值,因此采用NMF分析基因DNA的分子序列可使分析结果更加可靠。同样,用NMF来选择药物成分还可以获得最有效的且负作用最小的新药物。
其他应用此外,NMF算法在环境数据处理、信号分析与复杂对象的识别方面都有着很好的应用。近年来采用NMF思想的应用才刚展开,相信以后会有更多的成功应用。这些成功的应用反过来也将促进NMF的进一步研究。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国