梯度寻优,指沿某点函数变化率最小的梯度方向进行一维搜索,求得该方向上的极小点,再从该点出发沿新梯度方向搜索。循此进行,直到满足一定的精度要求,达到最优点。该法的优点是优化速度快。常用的梯度寻优方法为最小梯度下降法。
定义梯度寻优,指沿某点函数变化率最小的梯度方向进行一维搜索,求得该方向上的极小点,再从该点出发沿新梯度方向搜索。循此进行,直到满足一定的精度要求,达到最优点。该法的优点是优化速度快。常用的梯度寻优方法为最小梯度下降法。1
梯度下降法梯度下降法(英语:Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
描述梯度下降方法基于以下的观察:如果实值函数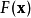 在点
在点 处可微且有定义,那么函数
处可微且有定义,那么函数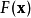 在
在 点沿着梯度相反的方向
点沿着梯度相反的方向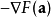 下降最快。
下降最快。
因而,如果
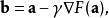 对于
对于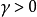 为一个够小数值时成立,那么
为一个够小数值时成立,那么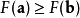 。
。
考虑到这一点,我们可以从函数F的局部极小值的初始估计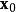 出发,并考虑如下
出发,并考虑如下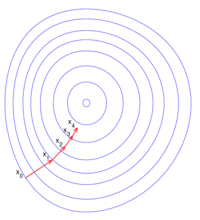 序列
序列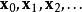 使得
使得
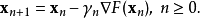 因此可得到
因此可得到
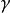
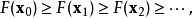 如果顺利的话序列
如果顺利的话序列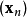 收敛到期望的极值。注意每次迭代步长可以改变。
收敛到期望的极值。注意每次迭代步长可以改变。
右侧的图片示例了这一过程,这里假设F定义在平面上,并且函数图像是一个碗形。蓝色的曲线是等高线(水平集),即函数F为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。(一点处的梯度方向与通过该点的等高线垂直)。沿着梯度下降方向,将最终到达碗底,即函数F值最小的点。2
参阅共轭梯度法
随机梯度下降法
本词条内容贡献者为:
张磊 - 副教授 - 西南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国