容许区间指的是总体中绝大多数个体观察值可能出现的范围。严格说,总体中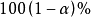 个体某种指标的所在范围,称为该指标的
个体某种指标的所在范围,称为该指标的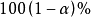 容许区间(在回归分析中亦称预测区间)。
容许区间(在回归分析中亦称预测区间)。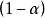 称为个体某指标值落人该范围的可信度2。
称为个体某指标值落人该范围的可信度2。
正态分布中,当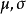 已知时,可通过标准正态变换
已知时,可通过标准正态变换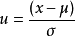 ,将正态变量值
,将正态变量值 变换为标准正态变量值
变换为标准正态变量值 ,于是:
,于是:
(1) 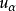 为双侧界值时:按标准正态变量值的分布规律
为双侧界值时:按标准正态变量值的分布规律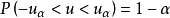 ,有
,有
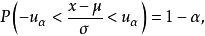 从而推导出:
从而推导出:
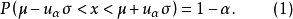
式(1)表示正态变量值 以
以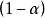 的概率落在式(2)的范围内。式(2)为正态变量值
的概率落在式(2)的范围内。式(2)为正态变量值 的双侧
的双侧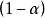 容许区间计算公式。
容许区间计算公式。
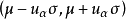 ,缩写为
,缩写为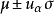 (式中
(式中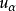 为双侧u界值)
为双侧u界值) 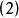
(2)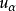 为单侧界值时:按标准正态变量值的分布规律
为单侧界值时:按标准正态变量值的分布规律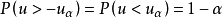 ,有
,有
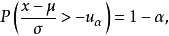 或
或
 从而推导出:
从而推导出:
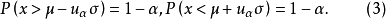 式(3)表示正态变量值
式(3)表示正态变量值 以
以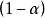 的概率落在式(4)的范围内。式(4)为正态变量
的概率落在式(4)的范围内。式(4)为正态变量 的单侧
的单侧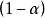 容许区间计算公式。
容许区间计算公式。
 或
或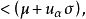 (式中
(式中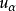 为单侧
为单侧 界值)。
界值)。 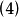
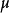 和
和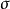 一般未知,常用大样本资料的
一般未知,常用大样本资料的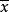 和
和 分别作为
分别作为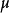 和
和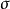 的估计值,所计算的容许区间称为参考值范围(reference range)。所谓参考值,是从总体中抽取一部份个体组成参考样本(简称样本),观测样本中每一个个体的某指标而得到的统计量。从概率角度看,因为个体变异的关系,如用单一参考值(点估计值)作为判断标准的可靠程度达很差的,为提高判断的可靠度,所以,需要定出一个参考值范围(区间估计范围)。
的估计值,所计算的容许区间称为参考值范围(reference range)。所谓参考值,是从总体中抽取一部份个体组成参考样本(简称样本),观测样本中每一个个体的某指标而得到的统计量。从概率角度看,因为个体变异的关系,如用单一参考值(点估计值)作为判断标准的可靠程度达很差的,为提高判断的可靠度,所以,需要定出一个参考值范围(区间估计范围)。
下面用正态分布法求参考值范围。
正态分布法适用于正态或近似正态分布资料2。
(1)正态变量 的双侧
的双侧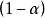 参考值范围计算公式:
参考值范围计算公式:
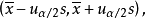 缩写为
缩写为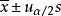 ,
, 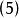
(2)正态变量 的单侧
的单侧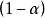 参考值范围为:
参考值范围为:
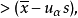 或
或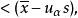
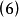
式(5)和式(6)中的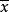 和
和 均由大样本算得。常用
均由大样本算得。常用 界值见表1。
界值见表1。
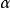 | 单侧 | 双侧 |
| 0.01 | 2.326 | 2.576 |
| 0.05 | 1.645 | 1.960 |
| 0.10 | 1.282 | 1.645 |
| 0.20 | 0.842 | 1.282 |
为方便起见,下面列出常用求正态分布资料95%参考值范围的方法及计算公式3:
双侧95%的界限值为: 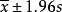 ;
;
单侧95%的上限值为: 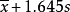 ;
;
单侧95%的下限值为: 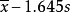 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国