[科普中国]-样本值

概念与定义

在数理统计中，要了解总体数据的分布规律，需要从总体中抽取一部分个体进行观测。在抽样过程中，每抽取一个个体，就是对总体X进行一次随机试验，抽取的n个个体X1,X2,…,Xn，称为总体X的一个容量为n的样本，样本中所包含的个体数量称为样本容量。1

样本值：X1,X2,…,Xn，是n个随机变量，抽取之后的观测数据x1,x2,…,xn，称为样本值或子样观察值。1

样本特性（1）代表性

子样X1,X2,…,Xn的每个分量Xi，与总体X具有相同的概率分布。2

（2）独立性

每次抽样的结果既不影响其余各次抽样的结果，也不受其他各次抽样结果的影响。2

常用统计量例举样本的平均值称为样本均值，样本偏离样本均值的平方的平均值称为样本方差。样本方差的算术平方根称为样本均方差。k阶原点矩是指随机变量偏离原点的距离的k次方的期望值，k阶中心矩是指随机变量偏离其中心的距离的k次方的期望值。2

（1）样本均值：；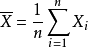

（2）样本方差：；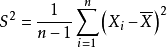

（3）样本均方差或标准差：；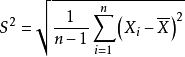

（4）样本的K阶原点矩：；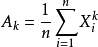

（5）样本的K阶中心矩：；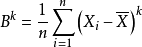

应用用样本来估计总体，通过对样本特征的研究来估计总体的特征。这种概率统计的方法在市场调研、金融评估等方面有广泛的应用。2