气体处于热动平衡时,气体分子的数目按速度大小分布的定律。
定义当温度一定时,气体分子速率平方的平均值是一定的。在任何一瞬间,分子的速率大小可能有许多值:有些分子速率为零;而同时又有一些分子的速率比平均速率大得多。究竟某一速率内的分子有多少个,另一速率内的分子又有多少个,可由分子速率分布来说明。当分子数目很大时,速率的分布必然服从一定的统计规律,即速率分布定律。首先由麦克斯韦从理论推出其公式,气体分子速率分布定律的公式,称为麦克斯韦速率分布定律。
历史1859年,J.C.麦克斯韦首先获得气体分子速度的分布规律,尔后,又为L.玻耳兹曼由碰撞理论严格导出。处于平衡状态下的理想气体分子以不同的速度运动,由于碰撞,每个分子的速度都不断地改变,使分子具有各种速度。因为分子数目很大,分子速度的大小和方向是无规的,所以无法知道具有确定速度U的分子数是多少,但可知道速度在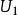 与
与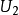 之间的分子数是多少。它表明:气体在宏观上达到平衡时,虽然个别分子的速度一般都不相同,并且由于相互碰撞而不断发生变化,但平均来说,速度在某一范围内的分子数在总分子数中所占的百分比总是一定的;该比值只与气体的种类及温度有关。1
之间的分子数是多少。它表明:气体在宏观上达到平衡时,虽然个别分子的速度一般都不相同,并且由于相互碰撞而不断发生变化,但平均来说,速度在某一范围内的分子数在总分子数中所占的百分比总是一定的;该比值只与气体的种类及温度有关。1
函数式的推导通过玻尔兹曼能量分布定律,我们很容易导出了分子按速度分布的函数式来,因为分子的动能与其速度之间有如下的关系:
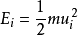 (1-1)
(1-1)
首先考虑分子在一维空间内沿x方向运动的速度分布情况:设分子的质量为m,它在x方向上的速度分量为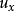 ,现将
,现将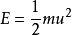 代入得:
代入得:
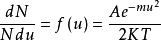 (1-2)
(1-2)
上式即为速度分布函数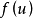 的表达式,速度分布函数又称为几率密度。
的表达式,速度分布函数又称为几率密度。
如果将上式在全部速度范围内进行积分,应用归一化条件(即分子在全部速度范围内出现的几率总和应等于1),便可求得上式中的常数A。归一化条件表示如下:
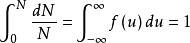 (1-3)
(1-3)
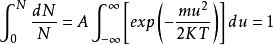 (1-4)
(1-4)
运用以下的标准积分结果:
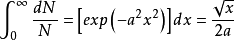 (1-5)
(1-5)
其中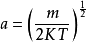 可得(1-4)式的解:
可得(1-4)式的解:
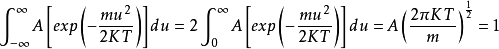 (1-6)
(1-6)
所以
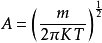
将A值代入(1-2)式中,即得速度分布函数如下:
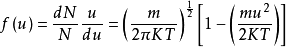 (1-7)
(1-7)
上式称为Maxwell-Boltzmann速度分布定律,式中的T为绝对温度,K为玻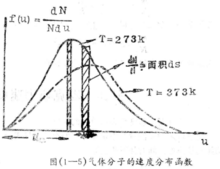 尔兹曼常数(
尔兹曼常数(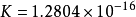 尔格/度)。
尔格/度)。
下面我们用图形来说明速度分布函数的几何意义:以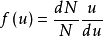 和u作图,得到右图1所示的曲线,函数
和u作图,得到右图1所示的曲线,函数 表示该曲线的方程式,曲线下方的窄长阴影面积,表示在速度u的附近的单位区间内出现的分子数(dN)占总分子数N的百分率,曲线覆盖的总面积表示分子所占的百分率之总和,该总和应等于1(因为
表示该曲线的方程式,曲线下方的窄长阴影面积,表示在速度u的附近的单位区间内出现的分子数(dN)占总分子数N的百分率,曲线覆盖的总面积表示分子所占的百分率之总和,该总和应等于1(因为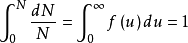 )。
)。
例如氮气分子(分子量为28)在一维空间内运动的分布函数,表示在右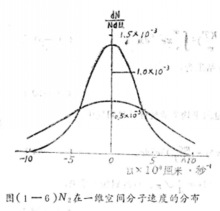 图2中,在25℃和在1025℃两种温度下,A值分别为
图2中,在25℃和在1025℃两种温度下,A值分别为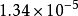 秒/厘米和
秒/厘米和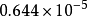 秒/厘米。由于分子运动正向和反向的机会相等,曲线呈对称形状,其最可几速率为零。2
秒/厘米。由于分子运动正向和反向的机会相等,曲线呈对称形状,其最可几速率为零。2
二维相与三维相的速度分布函数在二维空间内分子按速度分布的规律,依上述方法可求得速度分布函数如下:
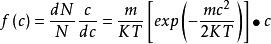 (1-8)
(1-8)
式中的c表示分子在x、y两个方向上的速度分量u和v的组合。当u和v的增量为du和dv时,净速度c由增至c+dc。氮分子在x、y两个方向上的速度分布曲线如图3所示。
在三维空间内所得的分子速度分布定律表示如下:
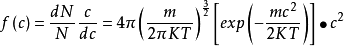 (1-9)
(1-9)
式中的c表示分子在x、y、z三个方向上的速度分量u、v、w的组合。当u、v、w获得增量du、dv、dw时,速度c相应的由c增加至c+dc。
右图3中的分布曲线,其两端几近于横轴并具有一个极大点,这表明速度最大和 最小的分子数目较少,而具有中等速度的分子占总分子数的分数为最大。与曲线的极大点相对应的速度即为最可几速度,用符号
最小的分子数目较少,而具有中等速度的分子占总分子数的分数为最大。与曲线的极大点相对应的速度即为最可几速度,用符号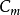 来表示。分布函数f(c)与温度和速度的数值有关,我们比较图中的两条曲线可以看出:当温度升高时,曲线的峰值降低并向高速方向移动,这意味着在分子总数目不变的情况下,具有较大速度的分子所占的分数,随温度的升高而增大,由于分布函数与速度呈负指数关系,当速度增大时,速度大的分子所占的分数迅速的下降,但在给定速度下的分子出现几率,具有确定不变的数值。2
来表示。分布函数f(c)与温度和速度的数值有关,我们比较图中的两条曲线可以看出:当温度升高时,曲线的峰值降低并向高速方向移动,这意味着在分子总数目不变的情况下,具有较大速度的分子所占的分数,随温度的升高而增大,由于分布函数与速度呈负指数关系,当速度增大时,速度大的分子所占的分数迅速的下降,但在给定速度下的分子出现几率,具有确定不变的数值。2
本词条内容贡献者为:
王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国