[科普中国]-爆破压力

概述

爆破压力（burst pressure）是对压力容器施加压力载荷使其发生破裂时的压力值。可以根据材料的拉伸强度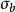 及屈服点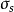 数据，并根据容器的几何尺寸来计算或估算出爆破压力。一般工程上较多采用带有经验性的并有较小误差的福贝尔式：爆破压力 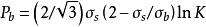。式中K为容器外径与内径的比值。K值小于1.1时的薄壁圆筒形容器，也可采用中径公式估算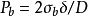： ，式中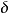 为实际壁厚，D为容器的平均直径（中径）。采用塑性理论也可以根据材料的扭转试验的剪切性能进行较精确的计算但计算较为复杂。1

爆破压力计算常用的公式就是著名的福贝尔（Faupel）式，爆破压力下限式为

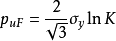
同理，爆破压力上限式为

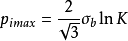
一般容器实际爆破力介于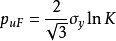式 和式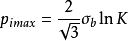 两者之间，并随材料的屈强比 v成线性变化，于是有

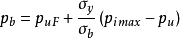
或

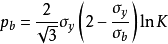
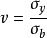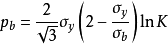令 ，则式 变为

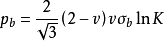
为了研究方便，将式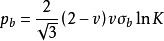 分为两个部分，即

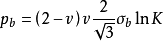
这样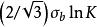， 显然表示理想塑性材料的极限压力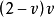； 则表示材料的屈强比对极限压力的影响。因 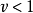，故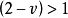 。这就说明由非理想塑性材料制造的圆柱壳的极限压力（爆破压力）比由模型化的理想塑性材料制造的圆柱壳的极限压力要大的原因。

近年来在使用福贝尔公式时也出现计算结果误差问题，尤其是对中等强度钢制高压容器经过试验后发现此式的误差超过15%～20%，有时高达30%，有人用一种比式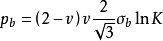 更为简化的但精确度比较高的最大压力计算式：

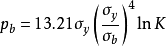
据称该式的误差在8%左右。2

气瓶动态爆破压力预测焊接气瓶是用于充装液氨、液氯、环丙烷、液化石油气等低压液化气体和溶解乙炔气体的可重复充装而无绝热装置的移动式压力容器。其使用广泛、数量大、流动性大、管理分散、使用环境恶 劣，充装介质大都具有易燃、易爆、剧毒、强腐蚀等性质。所以，气瓶在为经济发展作出贡献的同时，也存在着一定的安全隐患。近年来，存在着超期未检气瓶、超期服役气瓶供应市场的情况，安全隐患非常突出，气瓶爆炸事故时有发生。

事故发生后，在分析事故原因过程中，需要对事故过程进行模拟，计算爆破压力。对于气瓶静态爆破压力的模拟研究较多，1957 年，COOPER 就发表了关于预测气瓶静态爆破压力的论文，并提出一个解析方程来预测由各向同性塑性材料制成的钢瓶的静态爆炸压力，这个方程得到了理想的爆炸压力、材料属性、原始尺寸和材料极限抗拉强度的关系。随后，相继建立起基于弹性理论、 弹塑性理论、塑性理论，适用于薄壁、厚壁、单层、 多层，内、外壁存在腐蚀缺陷等不同条件下的气瓶静态爆破压力模型。

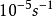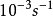静态爆破常用于模拟分析气瓶的水压或气压爆破，其爆破形式与气瓶爆炸还是有很大区别的。 由于水压或气压爆破升压速度较缓慢，气瓶受载荷作用时间长，应变速率低，可以看作是静态或准静态过程。按照应变速率划分，当应变速率低于 时称为静态变形;；介于 时 称为准静态变形；高于 时称为动态变形。

通常，随着应变速率的提高，材料的屈服强度和抗拉强度提高，延伸率降低，出现屈服滞后及断裂滞后等现象。要研究气瓶的爆炸过程，就需掌握气瓶材料相关的动态力学行为，因为相关动力学性能数据将为运用动力学模型对爆炸过程进行模拟提供更为准确的边界条件，提高模拟结果的精确性。

通过试验获得，对不同加载速率下的气瓶爆破压力进行了预测，并与修正后的经验公式计算得到的结果进行对比，得到以下结论：

（1）随着拉伸速率增加（从0.05 到 200 mm/s）， 抗拉强度和屈服强度提高（从 469. 2 到517. 9 MPa，从332.2 到392 MPa）。

（2）有限元气瓶爆破动态模拟分析结果表明，对气瓶加载，筒体和封头都发生变形，最终在筒体处发生破裂。随加载速率的增加，气瓶爆破时产生的塑性变形减小，应力增加，爆破时间减少，爆破压力增加。

（3）随加载速率的增加，有限元模拟分析得到的爆破压力与使用修正后的巴洛公式估算得到的爆破压力逐渐接近，所以动态快速加载条件下，可用该公式对爆破压力进行预测。3