[科普中国]-微分包含系统

简介数学分析中的微分包含式（Differential inclusion）是指具有如下形式的常微分方程式：

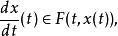
其中F(t,x)表示了一个集合，而非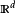空间中一个点。对微分包含式的研究源于微分不等式、投影动态系统、动态摩擦力问题和模糊集算法问题等不同的领域。

举例来讲，由库仑摩擦力的基本定理得知物体受到的摩擦力的大小为μN，方向与滑动方向相反，其中N是正向力，μ是摩擦系数。然而，在一个动态问题中，物体滑动量为0时受到的摩擦力可以是相应的受力平面内的小于等于μN任意的力，在这种情形下表示摩擦力与物体的位置、速度的函数关系就需要采用多值函数1。

理论现有的关于微分包含式的理论通常假定F(t,x) 是关于x的“上半侧连续”函数，t可测，且F(t,x) 对于所有的x、t都是闭合的凸集。

在以上假定的条件下，有关于初值问题:

在充分小的时间间隔[t0,t0+ε),ε>0 内

的解的存在定理。若对F作进一步约束，可以得到全局状况下的解的存在定理

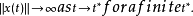
当F(t,x) 是非凸的集合时，相应的微分包含式的解的存在定理是目前的一个研究热点2。

应用微分包含式可以被适宜地理解为非连续的常微分方程，它出现在力学系统中对动态摩擦力的研究，以及电力电子领域中对理想开关的研究等。

微分包含系统的研究内容包括：它的不变集、回归集、吸引集、极限环、可达集的性质和计算，以及最优控制变量u的选择。分析方法主要基于集值映射和存活理论等3。