[科普中国]-最小费用流问题

简介

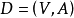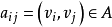在一个网络 中，弧 有容量上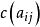界 和下界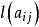 ，即单位流量的费用 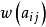。另外，每一个顶点 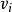都有一个货物供需量 ：

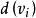当它大于0时，表示该点可供给一定量的货物；

当它小于0时，表示该点需求一定量的货物；

当它为0时，表示该点既不需要也不能提供货物，这样的点可以作为货物的中转点。

另外，假设网络中供需是平衡的。

网络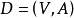 中的一个可行流是满足以下流量守恒和约束条件的函数

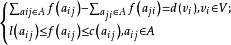
最小费用流问题是求一个可行流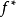使其费用最小，即

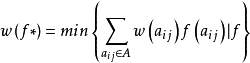
该问题存在多项式时间算法。

多项式时间算法[polynomial-time algorithm]

若一个算法的计算时间不超过其所求解问题的输入长度的一个多项式，则称该算法为多项式时间算法；其中计算时间和输入长度是以确定性图灵机为计算模型。通常认为只有多项式时间算法是可以求解大规模的实际问题，故多项式时间算法也称好算法或者有效算法。

若一个问题多输入仅限定于整数，而求解该问题多算法A的计算时间不超过其输入长度和其中整数的最大绝对值的一个多项式，则称A为伪多项式时间算法，比如，背包问题****和划分问题，则可以认为它是理论上相对容易求解的困难问题。1