[科普中国]-一阶拟线性偏微分方程

一阶拟线性偏微分方程(quasi-linear partial differential equation of first order)是一类特殊的一阶非线性偏微分方程，关于未知函数的偏导数是线性的一阶非线性偏微分方程称为一阶拟线性偏微分方程。

基本介绍一阶拟线性偏微分方程是一类特殊的一阶非线性偏微分方程。关于未知函数的偏导数是线性的一阶非线性偏微分方程称为一阶拟线性偏微分方程，一阶拟线性偏微分方程通常可以写成下列形状

其中和为和的已知连续可微函数，

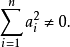其几何意义为，在维空间中的每一点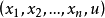给定了一个方向，曲面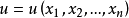在该点上的法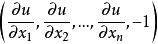方向

与方向正交，或者说，曲面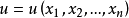在该点与此方向相切。常微分方程组

或

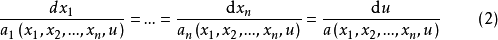称为上述一阶拟线性偏微分方程的特征方程。特征方程的积分曲线，或向量场的积分曲线称为该一阶拟线性偏微分方程的特征线1。

求解问题假设在变量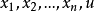的维空间的某一区城D，和为其变量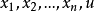的可微函数。

已给变量的任一函数，若此函数对这些变量都有偏导数，且能使方程(1)化为恒等式，则称此函数为方程(1)的解。和线性方程一样，可以把此解解释为空间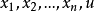中的曲面。

让方程(1) 和下列线性方程

相对应。

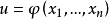定理1设为方程(3) 的解，设方程在变量的区域G决定了某一可微函数，且设在G内，则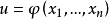是方程(1) 的解。

和线性情况不同，在拟线性情况，特征线不在空间，而在空间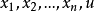，所以这时特征线另有几何意义，有下列事实。

定理2每一积分曲面按下述意义由特征线组成：经过此曲面的每一点可引某一条完全位于其上的特征线2。

为了求解方程(1)，应该按照下列方式进行。组成方程组(线性方程(3)的特征线方程组)：

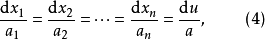(把方程组(4) 的积分曲线，即线性方程(3)的特征线称为拟线性方程(1)的特征线)对此方程组求积分，求出n个独立的第一积分：

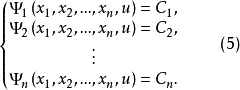
方程(1)的通积分可以这样写出：

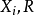其中是任意可微函数，这时假设函数是连续可微的，在所研究的变量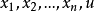的变化区域内不变为03。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学