[科普中国]-伯努利拓扑

伯努利拓扑（Bernoulli topology）是X上的拉东测度M(X)上的一种拓扑。

简介伯努利拓扑是X上的拉东测度M(X)上的一种拓扑。1

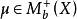记为Mb(X)的正元素全体所组成的子集，中测度网(μα)α∈A按伯努利拓扑收敛于的充分必要条件是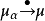且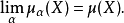

拓扑拓扑是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的一个学科。

设X是一个非空集合，X的幂集的子集（即是X的某些子集组成的集族）T称为X的一个拓扑。当且仅当：

1．X和空集都属于T；

2．T中任意多个成员的并集仍在T中；

3．T中有限多个成员的交集仍在T中。

称集合X连同它的拓扑τ为一个拓扑空间，记作(X,T)。

拉东测度拉东测度是一种正则测度。抽象测度的简称，即非负可列可加的集函数，测度论研究的对象。

拉东在变分法、实变函数、泛函分析、微分几何、相对论的数学理论等方面都有所贡献，他利用变分法研究微分几何以及对数位势的狄利克雷问题，发现了在数论中有重要应用的拉东曲线;还得到很有价值的拉东变换;在实变函数论中，引入了可包含勒贝格积分和斯蒂尔切斯积分的拉东积分，使积分概念得到进一步推广。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所