[科普中国]-随机对策

简介

随机对策是一类带有随机因素的多步对策。

随机对策[stochastic game] 随机对策的框架如下：

状态空间是一个可测空间。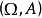

对任意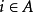，第 i 个局中人的行动空间是可测空间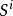，记。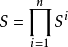

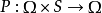是一个转移概率，对任意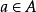，P(a/ω，s)表示今天的状态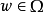为，行动为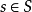时明天的状态为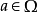的概率。

对任意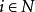，第 i 个局中人的支付函数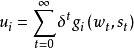，其中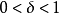为折扣因子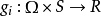，是第 i 个局中人的阶段支付函数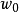，为初始状态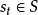，为阶段 t 时的行动，状态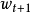由转移概率和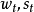确定。

对策论[game theory]

对策论亦称博弈论，是运筹学的一个重要分支。它所研究的是n(n≥2)个决策者在某种对抗或竞争的局势下，如何各自作出决策，从而使自己得到自己尽可能最有利的结果。

1944年，冯·诺依曼(J.von Neumann)和莫根施特恩(O.Morgenstern)出版了《博弈论与经济行为》一书，宣告了对策论的诞生，也奠定了对策论的基础。

1944年，诺贝尔经济奖授予纳什(J.F.Nash)等3位对策论学者，从而确认了对策论对经济论对核心重要性。

除此之外，对策论在政治学、军事学、心理学、生物学等领域都有非常广泛和深刻的应用。1

多步对策[multistep game]

多步对策指局中人的每个策略须由多次行动实现的对策。在多步对策中，每个局中人的策略由一系列行动所组成。通常，局中人最初选择的只是他的一个策略中的某一具体行动，在其他局中人选择了他们的策略中的某一行动后，这个局中人再采取新的行动，直到对策结束。

例如，象棋、桥牌比赛等均可视为多步对策。