[科普中国]-更新密度

概念

更新密度(renewal density)是一种导数。更新函数的导数：1

称为更新密度。它有如下的概率解释：对于很小的Δt>0，m(t)Δt近似地给出在区间(t，t+Δt)中的平均更新次数。

更新函数更新函数是一种数学期望。更新过程{N(t)，t≥0}在区间(0，t]中的更新次数的数学期望M(t)=E[N(t)](作为变元t的函数)称为更新函数。

更新过程更新过程是一类随机过程。是描述元件或设备更新现象的一类随机过程。设对某元件的工作进行观测。假定元件的使用寿命是一随机变量，当元件发生故障时就进行修理或换上新的同类元件，而且元件的更新是即时的(修理或更换元件所需的时间为零)。如果每次更新后元件的工作是相互独立且有相同的寿命分布，令N(t)为在区间(0，t]中的更新次数，则称计数过程{N(t)，t≥0}为更新过程。在数学上更新过程可简单地定义为相邻两个点事件(即更新)的间距是相互独立同分布(但从原点到第一次更新的间距T1可以有不同分布)的计数过程。根据T1的分布情形更新过程又分为普通更新过程，延迟更新过程和平衡更新过程三类。更新过程也可用过程的事件间距序列{Tn，n≥1}给定，这时N(t)和Tn有如下关系∶N(t)=sup{n：Sn≤t}和Sn=inf{t：N(t)=n}，其中：2

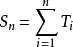是第n次更新时间(n≥1，再定义S0=0)。对于普通更新过程，Sn是n个相互独立同分布的非负随机变量之和，因此在数学上更新过程也可以看做是一类特殊的独立随机变量和。

随机过程随时间推进的随机现象的数学抽象。设(Ω，ℱ，P)为概率空间，T为指标t的集合，如果对每个t∈T，有定义在Ω上的实随机变量X(t)与之对应，就称随机变量族X={X(t)，t∈T}为一随机过程。

人们对一些特殊的随机过程早有研究。1907年前后，俄国数学家马尔可夫提出并研究一种能用数学分析方法研究自然过程的一般图式，后人称这种图式为马尔可夫链。1923年，美国数学家N.维纳从数学上定义了布朗运动，后来也称数学上的布朗运动为维纳过程。这种过程至今仍是随机过程的重要研究对象。通常认为，随机过程一般理论的研究于20世纪30年代才开始。1931年，原苏联数学家柯尔莫戈罗夫发表了《概率论的解析方法》;1934年，辛钦发表了《平稳过程的相关理论》。这两篇重要论文为马尔可夫过程和平稳过程奠定了理论基础。稍后，法国数学家莱维从样本函数角度研究随机过程，引进一般可加过程并研究了它的样本函数结构，他出版的关于布朗运动与可加过程的两本书中蕴含着丰富的概率思想。1953年，美国数学家J.L.杜布出版的著作《随机过程论》中系统且严格地叙述了随机过程的基本理论。他的工作推动了鞅理论的发展。1953年日本数学家伊藤清建立了关于布朗运动的随机微分方程的理论，定义了对布朗运动的一种随机积分——伊藤积分，为研究马尔可夫过程开辟了新的道路。近年来由于鞅论的进展，人们讨论了关于半鞅的随机微分方程，而流形上的随机微分方程理论正方兴未艾。20世纪60年代，法国学派基于马尔可夫过程和位势理论中的一些思想与结果，在相当大的程度上发展了随机过程的一般理论，包括截定理与过程的投影理论等，中国学者在平稳过程、马尔可夫过程、鞅论、极限定理、随机微分方程等方面都做出了较好的工作。

数学期望在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。

需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。

大数定律规定，随着重复次数接近无穷大，数值的算术平均值几乎肯定地收敛于期望值。

如果随机变量只取得有限个值或无穷能按一定次序一一列出，其值域为一个或若干个有限或无限区间，这样的随机变量称为离散型随机变量。3

概率论概率论是数学的一个分支，是研究随机现象的统计规律性的一门学科。在自然界和社会中，某种在固定条件下可能出现不同结果的现象称作随机现象(一个随机现象中可能发生也可能不发生的事件称为随机事件)。在这些现象中个别结果出现与否，具有偶然性。但在固定条件下重复实施多次，该事件发生的频率总是趋于一个固定的数值P。这一数值P就是随机事件的概率，它是事件发生可能性的度量。这种由大量观测得到的规律称为统计规律。统计规律是客观规律的一种，反映了事物内部固有的属性。例如，投掷一枚硬币，可能有两个结果：落地时正面朝上或者反面朝上。若不断重复投掷一枚硬币， 正面朝上和反面朝上的频率却是趋于1/2，这反映了硬币结构的均匀性;反之，若频率明显偏离1/2， 硬币结构必然是不均匀的。概率论作为一门科学是从17世纪开始的。法国的巴斯噶和费尔玛首先研究了概率论的基础。1713年端士的雅贝努利出版了概率论的第一本专著《猜度术》。1733年英国的德·穆阿佛尔发现正态概率曲线。1812年拉普拉斯出版了《分析概率论》，成为近代概率论的先驱。1902年法国数学家勒贝格创立的积分与测度理论，为近代概率论的发展奠定了基础。1933年苏联的柯尔莫哥洛夫提出概率论的公理化体系，提出并完成了著名的强大数定理的推论。公理化体系标志着概率论已成为一门成熟的数学学科，同时也是近代概率论的出发点。1942年N·维纳建立了统计动力学，使概率论进一步得到完善。近年来，概率论发展很快，形成了几个重大的分支，如极限定理、随机微分方程等。概率论在自然科学领域已起着巨大的作用，并且已被人们应用到社会科学领域，对于研究和揭示社会中大量随机现象及其规律性也有更重要的价值。