定时对策(game of timing)是一类特殊的两人无限零和对策,是单位正方形上的对策,局中人寻求纯策略表达和采取行动的时间选择。20世纪50年代,曾用这类对策解决了一些军事问题,特别是建立了一些空军战略和空战的模型,得出了一些有意义的结果。
基本介绍定义在单位正方形上的无限对策,如果它的支付函数取下列形式:
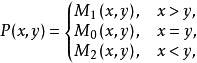 其中
其中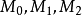 都是连续函数,但
都是连续函数,但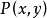 在正方形的对角线
在正方形的对角线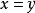 不连续,这种对策称为定时对策(games of timing)。
不连续,这种对策称为定时对策(games of timing)。
相关概念与分析定时对策的典型例子是决斗(duel)。假定有两个决斗者(局中人),每个局中人只有一粒子弹,在时间区间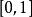 中开枪。开枪时间越晚,离对手越近,命中率越高。但是,离对手越近,被对手击中的可能性越大。因此,决斗双方都需选择一个最优策略——适当的时机开枪。这个例子可以用来描述军事战争,如决斗者换成空战双方只携带一枚导弹的战斗机;也可用来描述商业行动:如两个占有同一市场的寡头,双方都想把对手挤出市场,用降低价格的方法进行倾销。前者在第二次世界大战中得到充分研究,后者在40 年代和50 年代也有过不少研究。下面给出这一类对策的数学模型1。
中开枪。开枪时间越晚,离对手越近,命中率越高。但是,离对手越近,被对手击中的可能性越大。因此,决斗双方都需选择一个最优策略——适当的时机开枪。这个例子可以用来描述军事战争,如决斗者换成空战双方只携带一枚导弹的战斗机;也可用来描述商业行动:如两个占有同一市场的寡头,双方都想把对手挤出市场,用降低价格的方法进行倾销。前者在第二次世界大战中得到充分研究,后者在40 年代和50 年代也有过不少研究。下面给出这一类对策的数学模型1。
以“无声决斗”(silent duel)为例。两个局中人(决斗者)在相距2 时同时面向而行,每个局中人在时间单位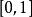 中只开枪一次,它不知道对手是否被击中,当局中人1在
中只开枪一次,它不知道对手是否被击中,当局中人1在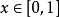 处开枪,击中对手的概率为
处开枪,击中对手的概率为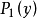 ,局中人2在
,局中人2在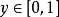 处开枪,击中对手的概率为
处开枪,击中对手的概率为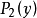 。
。
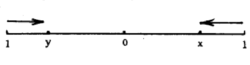
设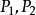 是连续单调减函数(距离越远,命中率越低),且
是连续单调减函数(距离越远,命中率越低),且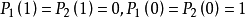 。如果局中人1击中对手而自己没有损伤(对手没开枪或者开枪没有命中)吗,其支付为1。
。如果局中人1击中对手而自己没有损伤(对手没开枪或者开枪没有命中)吗,其支付为1。
如果局中人1被击中,则支付为-1。如果双方打成平手,即同时没命中或同时命中,双方的支付均为0。该对策的支付函数为
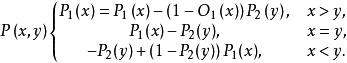 求解这个对策,从数学角度看来,其主要难点是
求解这个对策,从数学角度看来,其主要难点是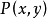 极可能在
极可能在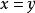 处不连续。为解决这个难题,这里引进
处不连续。为解决这个难题,这里引进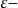 最优策略和sup-inf值概念。
最优策略和sup-inf值概念。
定义 设两人零和对策的支付函数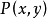 有界,如果
有界,如果
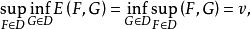 其中
其中
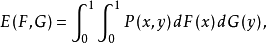 则称
则称 为该对策的sup-inf值。设
为该对策的sup-inf值。设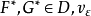 和
和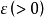 为实数,满足
为实数,满足
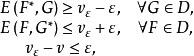 其中
其中 是对策的sup-inf值,则称F*和G*分别为局中人1和局中人2 的
是对策的sup-inf值,则称F*和G*分别为局中人1和局中人2 的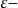 最优策略,
最优策略,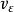 称为该对策的
称为该对策的 值1。
值1。
定理设单位正方形上对策的支付函数为
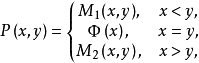
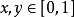 ,其中
,其中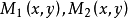 分别是定义在
分别是定义在
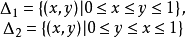 上的连续函数,满足
上的连续函数,满足
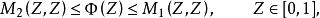 则该对策有sup-inf值,且对
则该对策有sup-inf值,且对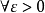 ,每个局中人至少有
,每个局中人至少有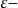 最优策略1。
最优策略1。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国