[科普中国]-复位势

概念

复位势是流体静力学的基本概念之一。指不可压缩流体平面无旋运动中，由速度势和流函数组成的解析函数。在不可压缩流体的平面无旋运动中，速度势φ与流函数ψ间满足柯西-黎曼条件：1

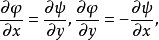
因此，复函数：

是复变量z=x+iy的解析函数。函数F的导数：

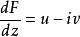
称为共轭复速度，它也是解析函数。共轭复速度沿某封闭曲线l的积分(沿反时针方向)为：

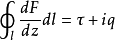
Γ是沿曲线l的速度环量，Q是从曲线l所围区域中流出的体积流量。当l所围的区域中无奇点，并且此区域为单连通时，Γ和Q都等于零。

无旋运动无旋运动是一种特殊流动。涡量处处等于零的流动称为无旋运动。在无旋运动中，必存在某标量场φ，其梯度等于流速，v=gradφ，φ称为速度势。速度势φ也可写成：

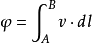
这里A是一个定点，可规定该点处的速度势的值为零；B是动点，积分沿任何连结A和B两点的曲线进行；dl是曲线上的微元向量。

流函数流函数是与质量守恒紧密联系的函数。在不可压缩流体的运动中，速度v需满足方程▽·v=0。因此必存在某向量函数B，使得v=▽×B，B称为广义流函数。在平面流动中，如取直角坐标系，有

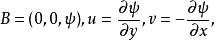
u和v是速度v在x方向和y方向的分量。函数ψ称为拉格朗日流函数。拉格朗日流函数有以下性质：

1.曲线ψ(x，y)=常数，是一条流线；

2.流函数沿某一方向的导数，等于从此方向顺时针旋转90°角方向上的速度分量；

3.两不同点上流函数之差，等于连结此两点的曲线(单位厚度的柱面)上的体积流量。

在不可压缩流体的轴对称流动中，流函数ψ与广义流函数B之间，在圆柱坐标系下有：

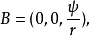
r是空间点到对称轴的距离。而在球坐标系下，则有：2

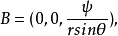
r是空间点到原点的距离，θ是纬度角。这时的流函数ψ称为斯托克斯流函数。在可压缩流体的定常流动中，广义流函数B与速度v之间的联系是ρv=▽×B， ρ是流体密度。

流体静力学研究处于静态的流体的力学分支(比较“流体动力学”〔hydrodynamics〕)。一般都认为是阿基米德首创。其应用包括贮存容器、闸门、水力装置和大坝的阀门等的设计。

流体力学的一个分支学科。流体静力学研究外力作用下流体相对静止时的平衡条件、有关物理量在流体中的分布及流体与边界之间的相互作用。研究流体静力学问题可以以刚化原理为基础。此原理认为：把流体中的任一部分刚化后，不会破坏流体原先的相对静止状态。相对静止的流体中，任一截面上的剪切应力都等于零，因此流体中的应力张量一定是球对称的。各分量可写成：3

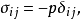
δij是克罗内克记号，p是压力。

解析函数能局部展成幂级数的函数，它是复变函数论研究的主要对象。解析函数类包括了数学及其在自然科学和技术应用中所遇到的大多数函数，这类函数关于算术、代数和分析的各种基本运算是封闭的，解析函数在其自然存在的域中代表唯一的一个函数，因此，对解析函数的研究具有特殊的重要性。

对解析函数的系统研究开始于18世纪。欧拉在这方面做出许多贡献。拉格朗日最早希望建立系统的解析函数理论，他曾试图利用幂级数的工具来发展这种理论，但未获成功。

法国数学家柯西以他自己的工作被公认为是解析函数理论的奠基者。1814年他定义正则函数为导数存在且连续，他批判了过去许多错误的结果，创立了若干法则，以保证级数运算的可靠性。1825年他得到了著名的柯西积分定理，随后又建立了柯西积分公式。柯西利用这些工具得到了正则函数在它的定义域内处处可表为收敛的幂级数的结果，其逆命题亦真。所以解析和正则是等价的。后来黎曼对柯西的工作做出了重要的发展。1900年，法国数学家古尔萨改善了正则函数的定义，只要求函数在定义域中处处有导数。

外尔斯特拉斯以幂级数为出发点开展对解析函数的研究。他定义正则函数为可以展开为幂级数的函数，创立了解析开拓理论，并利用解析开拓定义完全解析函数。柯西的方法限于研究完全解析函数的所谓单值分支，必须通过解析开拓才能和外尔斯特拉斯的理论统一起来。