[科普中国]-刘维尔方程

简介

在数学中，刘维尔方程（Liouville equation），又称刘维 - 布拉-盖尔芬德方程（Liouville-Bratu-Gelfandequation）是一个非线性特征值泊松方程，以数学家约瑟夫·利维尔（Joseph Liouville）、布拉图和以色列格尔芬德命名。方程式为：▽2ψ+λeψ=0。

此方程式出现在弗兰克 - Kamenetskii理论的热失控中以及钱德拉塞卡方程的天体物理学中。 这个方程还描述了发光线周围的空间电荷，并描述了行星状星云。1

刘维尔方程解在笛卡尔坐标（x，y）的二维平面中，约瑟夫·柳维尔在1853年提出了一个方程2，

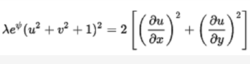
其中f（z）= u + iv是z = x + iy的任意分析函数。 1915年， Walker通过假设f（z）的形式找到了一个解。 如果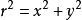，那么Walker的解

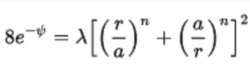
其中a是一些有限的半径。 这个解在任何n趋向的无穷远处衰减，但在n