.
牛顿法原理把非线性函数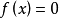 在
在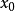 处展开成泰勒级数
处展开成泰勒级数
取其线性部分,作为非线性方程的近似方程,则有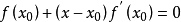
设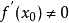 ,则其解为
,则其解为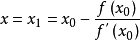
因为这是利用泰勒公式的一阶展开,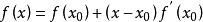 处并不是完全相等,而是近似相等,这里求得的
处并不是完全相等,而是近似相等,这里求得的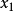 并不能让
并不能让 ,只能说
,只能说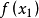 的值比
的值比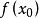 更接近
更接近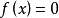 ,于是乎,迭代求解的想法就很自然了,
,于是乎,迭代求解的想法就很自然了,
再把f(x)在x1 处展开为泰勒级数,取其线性部分为 的近似方程,若
的近似方程,若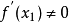 ,则得
,则得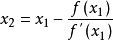 如此继续下去,得到牛顿法的迭代公式:
如此继续下去,得到牛顿法的迭代公式: ,通过迭代,这个式子必然在
,通过迭代,这个式子必然在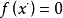 的时候收敛。整个过程如右图:
的时候收敛。整个过程如右图:
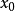 例1 用牛顿法求方程
例1 用牛顿法求方程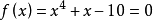 在
在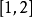 内一个实根,取初始近似值=1.5。 解
内一个实根,取初始近似值=1.5。 解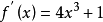 所以迭代公式为:
所以迭代公式为:
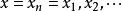 2
2
牛顿法运算方法导数法这里将简单介绍一下牛顿二阶导数法。对其几何意义及收敛性不作详细的叙述,读者可仿照牛顿法进行讨论。
将f(x)在x0处展开泰勒级数f(x)=f(x0)+f′(x0)(x-xo )+ f″(x0)(x- x) +…
取右端前三项近似代替f(x),于是得f(x)=0的近似方程为
f( )+f′( )(x- )+ f″( )(x- ) =0
也即f( )+(x- )[f′( )+ f″( )(x- )] =0 (3)
设其解为 .利用(1), - =- ,代入(3)中括号内 - ,则得f( )+( - ) [f′( )+ f″( ) ] =0
于是解出 ,得 = -
重复以上过程得: = -
于是得牛顿二阶导数法的迭代公式为:
= - n=0,1,2,… (4)
上式与牛顿法迭代公式(2)相比,利用此公式求根收敛更快,迭代次数更少。其缺点是要求f(x)的二阶导数存在。
切线法这是一个由开方公式引出的:
X(n+1)=Xn+(A/X^(k-1)-Xn)1/k (5)(n,n+1表示下角标)
开立方公式:
当(5)式中的K=3时就是开立方公式。
设A = X^3,求X.称为开立方。 开立方有一个标准的公式:
X(n+1)=Xn+(A/X^2-Xn)1/3 (n,n+1是下角标)
例如,A=5,,即求
5介于1的3次方;至2的3次方;之间(1的3次方=1,2的3次方=8)
初始值X0可以取1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,都可以。例如我们取X0 = 1.9按照公式:
第一步:X1=1.9+(5/1.9^2;-1.9)1/3=1.7。
即5/1.9×1.9=1.3850416,1.3850416-1.9=-0.5149584,-0.5149584×1/3=-0.1716528,1.9+(-0.1716528)=1.7。即取2位数值,,即1.7。
第二步:X2=1.7+(5/1.7^2;-1.7)1/3=1.71。
即5/1.7×1.7=1.73010,1.73-1.7=0.03,0.03×1/3=0.01,1.7+0.01=1.71。取3位数,比前面多取一位数。第三步:X3=1.71+(5/1.71^2;-1.71)1/3=1.709.
第四步:X4=1.709+(5/1.709^2;-1.709)1/3=1.7099
这种方法可以自动调节,第一步与第三步取值偏大,但是计算出来以后输出值会自动转小;第二步,第四步输入值
偏小,输出值自动转大。即5=1.7099^3;
当然初始值X0也可以取1.1,1.2,1.3,。。。1.8,1.9中的任何一个,都是X1 = 1.7 > 。当然,我们在实际中初始值最好采用中间值,即1.5。 1.5+(5/1.5²-1.5)1/3=1.7。
如果用这个公式开平方,只需将3改成2,2改成1。即
X(n + 1) = Xn + (A / Xn − Xn)1 / 2 (n,n+1是下角标)
例如,A=5:
5介于2的平方至3的平方;之间。我们取初始值2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9都可以,我们最好取 中间值2.5。 第一步:2.5+(5/2.5-2.5)1/2=2.2;
即5/2.5=2,2-2.5=-0.5,-0.5×1/2=-0.25,2.5+(-0.25)=2.25,取2位数2.2。
第二步:2.2+(5/2.2-2.2)1/2=2.23;
即5/2.2=2.272,2.272-2.2=-0.072,-0.072×1/2=-0.036,2.2+0.036=2.23。取3位数。
第三步:2.23+(5/2.23-2.23)1/2=2.236。
即5/2.23=2.242,2.242-2.23=0.012,0.012×1/2=0.006,2.23+0.006=2.236.
每一步多取一位数。这个方法又叫反馈开方,即使你输入一个错误的数值,也没有关系,输出值会自动调节,接近准确值。3
简化牛顿法为了减少牛顿法的计算量,在每步计算中用F'(x^0)代替F'(x^k),得简化牛顿程序:
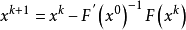 ,其中k从0开始取值。
,其中k从0开始取值。
于是由x^k计算x^(k+1)只需计算F(x^k),不再计算F'(x^k)及求逆,使每步计算量大大减少,这是此算法的优点,其缺点是收敛慢,只有线性收敛速度。
迭代法是方程求根最常用的方法,其基本思想是一种逐次逼近的方法。即首先给定一个粗糙的初始值,然后用同一个迭代公式反复校正这个初值,直到满足预先给出的精度要求为止,该方法的关键是如何构造一个合适的迭代表达式。
对于非线性方程f(X)= 0,牛顿法所构造的迭表达式为:
XN+ 1= XN-f(X)/f′(X)
牛顿法每迭代一次,都需要计算f'(X)的值,若f(X)比较复杂,计算f'(X)的工作量就可能很大,此时用一个给定的常数c来代替f'(X)值,这时迭代表达式就成为:
XN+ 1= XN-f(X)/c
这就是简化牛顿法迭代表达式,选取一个合适的c值代入上式,即可用此迭代表达式计算。4




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国