[科普中国]-局部截痕

局部截痕是揭示流在常点附近的局部性态所引进的概念，也是研究流的性质的一个有力的几何工具。

简介局部截痕是揭示流在常点附近的局部性态所引进的概念，也是研究流的性质的一个有力的几何工具。

设 f 是度量空间 M 上的流， N 是 M 的任一集合，T>0，记中

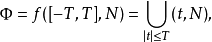
人们把 Φ 称为时间长度为 2T 的有限管。设 S 是 Φ 内的闭集，若对点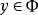 都存在惟一数值 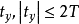，使得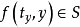 ，那么就称 S 是有限管 Φ 的局部截痕。

性质对常点而言，总存在含该点的有限管，使得它有含该常点的局部截痕存在，并由此得到，流在常点附近的轨弧与希尔伯特空间中一族平行线段同胚。

特别地，对于流形上由向量场（即常微系统）产生的流，它在常点附近的轨弧同胚于欧氏空间的一族平行线段.此外，这种流在非平凡周期点处的局部截痕的存在，可使对流在这周期轨道附近性质的研究转化为对在这截痕上所导出的庞加莱映射的研究。

局部截痕是由惠特尼(Whitney,H.)于1932年引入的。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学