简介
逆系统是非线性系统控制设计中的一种反馈线性化理论与方法。
令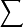 为因果关系系统,表示其传递关系的算子为
为因果关系系统,表示其传递关系的算子为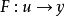 。如果可以找到另一因果关系系统
。如果可以找到另一因果关系系统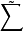 ,其传递关系算子为
,其传递关系算子为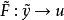 并有
并有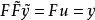 和
和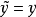 ,则称系统
,则称系统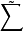 为系统
为系统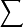 的逆系统。
的逆系统。
对非线性系统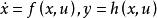 及适当的初态
及适当的初态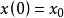 ,若存在系统
,若存在系统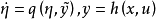 及适当初态
及适当初态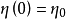 ,使得
,使得 ,则系统
,则系统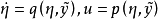 是系统
是系统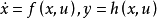 的逆系统。1
的逆系统。1
应用逆系统理论在控制理论的许多方面都有广泛的应用,如解祸、模型匹配、最小设计、多变量线性系统零点的定义与求解、多变量非线性系统设计的逆系统方法、编码理论、滤波、对策论等方面。
非线性系统[nonlinear system]
由非线性微分方程或差分方程描述的动态系统。若非线性系统中含有控制项,则称其为非线性控制系统。
一个控制系统的非线性可能来自受控系统本身,也可能由控制器设计中非线性元件所引起。控制理论中讨论最多的是两类非线性系统:一般非线性系统和仿射非线性系统。
在连续情况下一般非线性系统可表示为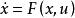 。
。
仿射非线性系统可表示为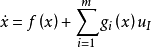 。
。
它对控制是线性的。可以说一般系统都是非线性的,而线性只是一种近似,也是一种特例。
从20世纪70年代开始发展起来的非线性系统几何理论,即用微分几何方法研究非线性系统,在系统结构分析和相关控制设计方面取得了很大成功,例如在反馈线性化和解耦等领域。在非线性系统等稳定性分析及镇定设计等方面也产生了许多新控制方法,例如基于能量的控制方法、反步法及滑动模控制等。由于几乎所有的实际系统都是非线性的,非线性系统的动态分析及其控制设计成为控制理论的主要研究目标。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国