设函数f的离散数据为(xi,yi),yi=f(xi),i=0,1,2,...,n,插值的目的是在x0,x1,x2,...,xn之间给定了自变量x的值后,要去求函数f的近似值,其途径是构造插值多项式,不同的构造方法,就是不同的插值法。与此相反,反插值的目的是在y0,y1,...,yn之间给定了函数f的值后,要去求自变量x的近似值,其途径仍是利用插值法。
反插值有两种处理方式:一种是直接利用函数f的插值多项式;另一种是在假设f-1存在的前提下,构造f的反函数f-1的插值多项式。因为反插值归结为求满足f(x)=c的x的近似值,这里c是在y0,y1,...,yn之间的某个值。如果f的反函数f-1存在,则x=f-1(c)。反插值就是求f-1在c上的近似值。当c=0时,反插值就是求函数f的近似零点,或者说是求方程f(x)=0的近似根,所以反插值有明显的意义1。
基本介绍反插值(inverse interpolation)是一种插值法,指利用插值函数反求满足某条件之自变量 的近似值。设给定函数
的近似值。设给定函数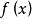 在
在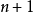 个不同点
个不同点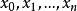 上的值
上的值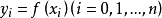 ,欲求使
,欲求使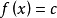 之
之 的近似值,这里
的近似值,这里 是含
是含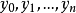 的区间[α,β]中之某个值。反插值就是求
的区间[α,β]中之某个值。反插值就是求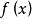 的反函数
的反函数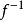 在c处的近似值2。
在c处的近似值2。
方法步骤求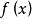 的反函数
的反函数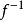 在c处的近似值通常可由
在c处的近似值通常可由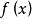 的牛顿插值公式,
的牛顿插值公式,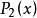 近似代替
近似代替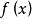 ,再令
,再令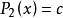 ,求出
,求出 的近似,一般用逐次逼近法,先取
的近似,一般用逐次逼近法,先取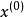 使得满足
使得满足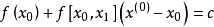 ,即
,即
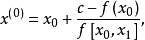 再求
再求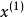 ,使它满足
,使它满足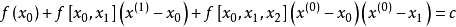 ,这里
,这里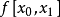 及
及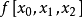 为
为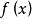 的一阶与二阶均差。由上式得到
的一阶与二阶均差。由上式得到
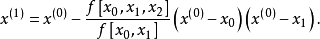 然后用迭代公式
然后用迭代公式
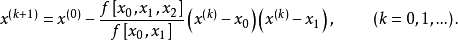 迭代至
迭代至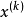 与
与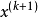 在所要求精度下相等为止。也可直接利用反函数
在所要求精度下相等为止。也可直接利用反函数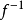 以
以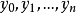 为节点的牛顿插值多项式
为节点的牛顿插值多项式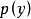 ,用
,用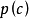 近似
近似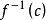 。
。
反插值及余项假设函数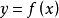 以表格形式给出如下:
以表格形式给出如下:
|| || 表1
反插值就是要以函数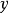 的值来求自变量
的值来求自变量 的的值。
的的值。
设函数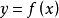 在含
在含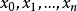 的区间
的区间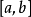 上严格单调,则由高等数学知识可知,
上严格单调,则由高等数学知识可知,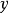 与
与 是一一对应的,即存在反函数
是一一对应的,即存在反函数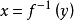 ,此时反插值问题有唯一解存在3。
,此时反插值问题有唯一解存在3。
一般情况下,可用拉格朗日插值多项式或牛顿插值多项式,只须将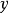 与
与 的位置互换即可。如用拉格朗日插值多项式对上表作反插值有
的位置互换即可。如用拉格朗日插值多项式对上表作反插值有
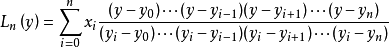 反插值的余项为
反插值的余项为
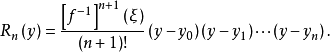
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国