[科普中国]-指数插值

指数插值(exponential interpolation)是常用的插值方法之一，指用指数函数之和作为插值函数的插值方法。例如，在分析放射性元素衰减时常被采用。

概念常用的插值方法之一。指用指数函数之和作为插值函数的插值方法。例如，在分析放射性元素衰减时常被采用。给出样点(xi，fi) (i=0，1，…，n)，及两两互异的实数λ0，λ1，…，λn，求：

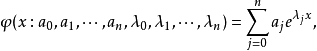使其满足插值条件：

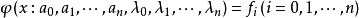此即指数插值问题。它归结为以a0，a1，…，an为未知数的线性方程组的求解问题。

插值插值是数值逼近的基本方法和主要研究方向。是从某函数的某些给定的离散点上的已知值或导数值出发补插出该函数的数值方法的总称，是函数数值逼近的重要组成部分。

给定函数f(x)在n+1个互异点的值f(xi)(有时还给定某些点的某些导数值)，i=0，1，…，n，在某函数类Φ中寻求函数φ(x)，使之φ(xi)=f(xi)(有时还要求在某些点处某些导数值相等)，则称之为插值问题。f(x)是待求的被插值函数，φ(x)被称为f(x)的插值函数。函数类Φ可以是不同函数类，如取Φ作代数多项式、有理函数、指数函数、三角多项式等，于是就相应有代数多项式插值、有理插值、指数插值、三角插值等不同类型的插值方法。

插值问题的主要研究内容是：给定被插函数f(x)的插值节点，插值函数类Φ，插值条件，满足插值条件的函数φ(x)(∈Φ)的存在性、惟一性和构造问题；插值函数作为被插函数的近似的误差估计问题；以及当插值结点逐渐加密，并相应扩充插值函数类的插值过程的收敛性和稳定性问题。

利用插值方法通过函数在有限个点处的取值状况估算出该函数在未知点处的值，是求近似值的最基本最常用的手段。中国刘焯早在公元6世纪就将等距二次插值用于天文计算。英国数学家、物理学家牛顿(Newton，I.)和格雷果里(Gregory，J.)于17世纪建立了等距节点上的插值公式；法国数学家、力学家拉格朗日(Lagrange，J.-L.)于18世纪给出了一般的非等距结点上的插值公式；他们应用插值公式于航海与天文计算中。许多现代数值计算方法都直接或间接地利用了在离散数据的基础上补插出连续函数的思想和方法，例如数值积分、有限差分方法、有限元法和有限体积方法等。1

指数函数指数函数是数学中重要的函数。应用到值e上的这个函数写为exp(x)。还可以等价的写为ex，这里的e是数学常数，就是自然对数的底数，近似等于 2.718281828，还称为欧拉数。

当a>1时，指数函数对于x的负数值非常平坦，对于x的正数值迅速攀升，在 x等于0的时候，y等于1。当00且a≠1。

数值逼近泛指数学计算问题的近似解法。狭义的理解则专指对函数的逼近，即对于给定的较广泛的函数类F中的函数y=f(x)，从较小的子类H中寻求在某种意义下f的一个近似函数h(x)，以便于计算和处理。

最早的数值逼近工作始于18世纪到19世纪初欧拉、拉普拉斯、傅立叶、庞斯列等人对一些个别函数的最佳逼近问题的研究工作，这些问题是从绘图学、测地学、机械设计等方面的实际需要中提出的。但当时没有形成深刻的概念和统一的方法。1854年，切比雪夫提出了最佳逼近的概念，研究了逼近函数类(H)是n次多项式时最佳逼近元的性质和判定定理。后来又与其学生在这方面得出许多重要的结果。1885年外尔斯特拉斯证明，原则上任何连续函数都可以用多项式以任何预先指定的精确度在函数的定义区间上一致地近似表示出来，开创了多项式逼近理论。如果考虑到怎样逼近才最好的问题，就得出最佳一致多项式逼近理论，这正好是切比雪夫的思想。可以说，切比雪夫和外尔斯特拉斯是现代数值逼近的奠基人。D.杰克森于1911年对逼近阶，即逼近的极小极大偏差当n增长时的下降速度进行研究，探讨逼近偏差与被逼近函数的构造(光滑性)的关系;次年，伯恩斯坦用逼近阶来反推被逼近函数的构造性质。他们有力地推动了数值逼近的发展。20世纪30年代中期，J.A.法瓦尔和柯尔莫戈罗夫开创周期可微函数类借助于三角多项式的最佳逼近的精确估计以及借助于傅立叶级数部分和的一致逼近的渐近精确估计的工作，把杰克森等的工作推向新的高度。从那时起，直到20世纪60年代，C.M.尼科利斯基等人在这方面继续取得重要的成果。从实际应用的角度看，要解决一个函数的最佳逼近问题，需要构造出最佳逼近元和算出最佳逼近值。一般地，要精确解决这两个问题十分困难，这促使人们为寻求最佳逼近元的近似表示和最佳逼近值的近似估计而设计出各种算法，例如列梅兹算法、极小极大(劳勃)算法、递推算法等。近20年来由于高速电子计算机的广泛应用，数值逼近的理论和方法发展迅速，成为计算数学和应用数学的重要分支，其结果被广泛用于构造数值积分、求函数零点、解微分方程和积分方程的近似方法等各种问题中。1

本词条内容贡献者为:

王海侠 - 副教授 - 南京理工大学